
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴相交于点C;直线l的解析式为y= x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3) 动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
1)解:连接AE.
由已知得:AE=CE=5,OE=3,
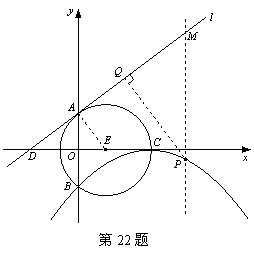 在Rt△AOE中,由勾股定理得,
在Rt△AOE中,由勾股定理得,
OA=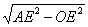 =
=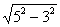 =4.
=4.
∵OC⊥AB,
∴由垂径定理得,OB=OA=4.
OC=OE+CE=3+5=8.
∴A(0,4),B(0,-4),C(8,0).
∵抛物线的顶点为点C,
∴设抛物线的解析式为y=a(x-8)2.
将点B的坐标代入上解析式,得
64 a=-4. 故 a=-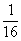 .
.
∴ y=-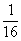 (x-8)2.
(x-8)2.
∴ y=-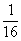 x 2+x-4 为所求抛物线的解析式.
x 2+x-4 为所求抛物线的解析式.
(2) 在直线l的解析式y=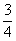 x+4中,令y=0,得=
x+4中,令y=0,得=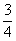 x+4=0,解得 x=-
x+4=0,解得 x=-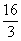 ,
,
∴点D的坐标为(-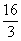 ,0);
,0);
当x=0时,y=4,所以点A在直线l上.
在Rt△AOE和Rt△DOA中,
∵ 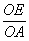 =
=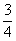 ,
,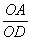 =
=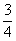 ,∴
,∴ 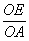 =
=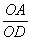 .
.
∵ ∠AOE=∠DOA=90°,∴ △AOE∽△DOA. ∴ ∠AEO=∠DAO.
∵∠AEO+∠EAO=90°,∴ ∠DAO+∠EAO=90°. 即 ∠DAE=90°.
因此,直线l与⊙E相切于点A.
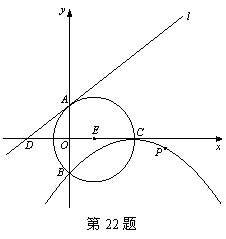
(3)过点P作直线l的垂线段PQ,垂足为Q;过点P作直线PM垂直于x轴,交直线l于点M.
设M(m,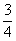 m+4),P(m,-
m+4),P(m,-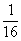 m 2+m-4). 则
m 2+m-4). 则
PM=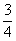 m+4-(-
m+4-(-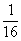 m 2+m-4)=
m 2+m-4)=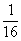 m 2-
m 2-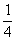 m+8=
m+8=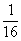 (m-2)2+
(m-2)2+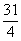 .
.
当m=2时,PM取得最小值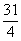 .
.
此时,P(2,-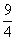 ).
).
对于△PQM,∵ PM⊥x轴,∴ ∠QMP=∠DAO=∠AEO. 又∵∠PQM=90°,
∴ △PQM的三个内角固定不变.
∴ 在动点P运动的过程中,△PQM的三边的比例关系不变.
∴ 当PM取得最小值时,PQ也取得最小值.
PQ最小=PM最小·sin∠QMP=PM最小·sin∠AEO=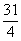 ×
×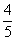 =
=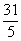 .
.
所以,当抛物线上的动点P的坐标为 (2,-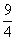 )时,点P到直线l的距离最小,其最小距离为
)时,点P到直线l的距离最小,其最小距离为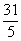


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
质检部门为了检测某品牌电器的质量,从同一批次共10 000件产品中随机抽取100件进行检测,检测出次品5件,由此估计这一批次产品中的次品件数是
A. 5 B. 100 C. 500 D. 10 000
查看答案和解析>>
科目:初中数学 来源: 题型:
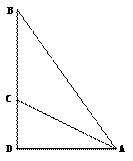
如图,斜面AC的坡度(CD与AD的比)为1:2,AC= 米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为2
米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为2
A.5米 B.6米 C. 8米 D.  米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
某学校初三年级男生共200人,随机抽取10名测量他们的身高为(单位:cm):
181、176、169、155、163、175、173、167、165、166.
(1)求这10名男生的平均身高和上面这组数据的中位数;
(2)估计该校初三年级男生身高高于170cm的人数;
(3)从身高为181、176、175、173的男生中任选2名,求身高为181cm的男生被抽中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
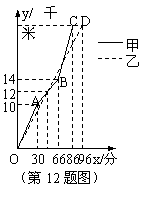
在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是
A.甲先到达终点
B.前30分钟,甲在乙的前面
C.第48分钟时,两人第一次相遇
D.这次比赛的全程是28千米
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
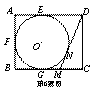
如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( )
A. 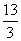 B.
B. 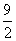 C.
C. 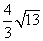 D.2
D.2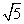
查看答案和解析>>
科目:初中数学 来源: 题型:
老师和小明同学玩数学游戏,老师取出一个不透明的口袋,口袋中装有三张分别标有数字1,2,3的 卡片,卡片除数字个其余都相同,老师要求小明同学两次随机抽取一张卡片,并计算两次抽到卡片上 的数字之积是奇数的概率,于是小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果,题 20图是小明同学所画的正确树状图的一部分.
(1) 补全小明同学所画的树状图;
(2) 求小明同学两次抽到卡片上的数字之积是奇数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com