练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知∠AOB=120°，点A绕点O顺时针旋转后的对应点A1落在射线OB上，点A绕点A1顺时针旋转后的对应点A2落在射线OB上，点A绕点A2顺时针旋转后的对应点A3落在射线OB上，…，连接AA1，AA2，AA3…，依此作法，则∠AAnAn+1等于______度．（用含n的代数式表示，n为正整数）

    【答案】.

    【解析】∵点A绕点O顺时针旋转后的对应点A1落在射线OB上，

    ∴OA=OA1，

    ∴∠AA1O=，

    ∵点A绕点A1顺时针旋转后的对应点A2落在射线OB上，

    ∴A1A=A1A2，

    ∴∠AA2A1=∠AA1O=，

    ∵点A绕点A2顺时针旋转后的对应点A3落在射线OB上，

    ∴A2A=A2A3，

    ∴∠AA3A2=∠AA2A1=，

    ∴∠AAnAn﹣1=，

    ∴∠AAnAn+1=180°﹣．

    故答案是：180﹣．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

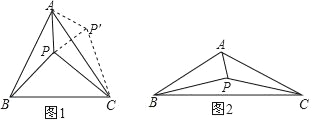
    【题目】在△ABC中，AB=AC，∠BAC=α，点P是△ABC内一点，且∠PAC+∠PCA=，连接PB，试探究PA、PB、PC满足的等量关系．

    （1）当α=60°时，将△ABP绕点A逆时针旋转60°得到△ACP′，连接PP′，如图1所示．由△ABP≌△ACP′可以证得△APP′是等边三角形，再由∠PAC+∠PCA=30°可得∠APC的大小为　 　度，进而得到△CPP′是直角三角形，这样可以得到PA、PB、PC满足的等量关系为　 　；

    （2）如图2，当α=120°时，参考（1）中的方法，探究PA、PB、PC满足的等量关系，并给出证明；

    （3）PA、PB、PC满足的等量关系为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了应对人口老龄化问题，国家大力发展养老事业．某养老机构定制轮椅供行动不便的老人使用．图①是一种型号的手动轮椅实物图，图②为其侧面示意图，该轮椅前后长度为120cm，后轮半径为24cm，CB=CD=24cm，踏板CB与CD垂直，横档AD、踏板CB与地面所成的角分别为15°、30°．求：

    （1）求横档AD的长；

    （2）点C离地面的高度．（sin15°=0.26，cos15°=0.97，精确到1cm）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图②所示，则当x＝4时，点R应运动到( )

    A. P处B. Q处C. M处D. N处

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，两座建筑物AB及CD，其中A，C距离为60米，在AB的顶点B处测得CD的顶部D的仰角β＝30°，测得其底部C的俯角α＝45°，求两座建筑物AB及CD的高度(保留根号)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．

    （1）求该抛物线的解析式；

    （2）当点P在直线BC上方时，请用含m的代数式表示PG的长度；

    （3）在（2）的条件下，是否存在这样的点P，使得以P、B、G为顶点的三角形与△DEH相似？若存在，求出此时m的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．

    （1）求证：四边形BFCE是平行四边形；

    （2）若AD=10，DC=3，∠EBD=60°，则BE= 时，四边形BFCE是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，晚上小亮在广场上乘凉，图中线段AB表示站在广场上的小亮，线段PO表示直立在广场上的灯杆，点P表示照明灯.

    请你再图中画出小亮在照明灯P照射下的影子BC；

    如果灯杆高PO=12m，小亮的身高AB=1.6m，小亮与灯杆的距离BO=13m，请求出小亮影子的长度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与实践

    数学活动课上，小红画了如图1所示的两个共用直角顶点的等腰直角三角形与等腰直角三角形，其中，，连接，、、分别为边、、的中点，连接、.

    操作发现：

    小红发现了：、有一定的关系，数量关系为_____________________________；位置关系为_________________.

    类比思考：

    如图2，在图1的基础上，将等腰直角三角形绕点旋转一定的角度，其它条件都不变，小红发现的结论还成立吗？请说明理由.（提示：连接、并延长交于一点）

    深入探究：

    在上述类比思考的基础上，小红做了进一步的探究.如图3，作任意一个三角形，其中，在三角形外侧以为腰作等腰直角三角形，以为腰作等腰直角三角形，分别取斜边、与边的中点、、，连接、、，试判断三角形的形状，并说明理由.

    查看答案和解析>>

    同步练习册答案