
| A. | 向左平移4个单位 | B. | 向右平移4个单位 | C. | 向上平移4个单位 | D. | 向下平移4个单位 |
分析 先由二次函数y=(x-2010)(x-2011)+4求出抛物线,然后求出抛物线与x轴的两个交点横坐标,利用坐标轴上两点间距离公式即可求得距离是1.
解答 解:二次函数y=(x-2010)(x-2011)+4
=[(x-2011)+1](x-2011)+4
设t=x-2011,则原二次函数为
y=(t+1)t+4
=t2+t+4
=(t+$\frac{1}{2}$)2-$\frac{1}{4}$+4
=(t+$\frac{1}{2}$)2+$\frac{15}{4}$.
则原抛物与x轴没的交点,只有抛物线向下平移才能使其与x轴交于两点,
若原抛物线向下平移4个单位,则新抛物的解析式为:
y=(t+$\frac{1}{2}$)2+$\frac{15}{4}$-4=(t+$\frac{1}{2}$)2-$\frac{1}{4}$.
则新抛物与x轴的交点距离为|0-(-1)|=1.
故选D.
点评 本题考查了函数图象的平移,抛物线与坐标轴的交点坐标的求法,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
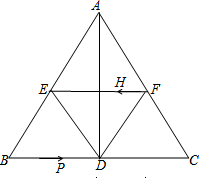 如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
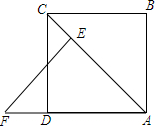 如图,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置
如图,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com