
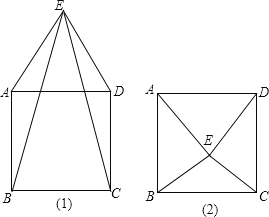
【题目】以正方形![]() 的边
的边![]() 作等边三角形
作等边三角形![]() ,则
,则![]() 的度数是______________
的度数是______________![]() .
.
【答案】30°或150°
【解析】
如果要求![]() 的度数,则要分两种情况讨论,第一种点
的度数,则要分两种情况讨论,第一种点![]() 在正方形
在正方形![]() 的内部,第二种情况点
的内部,第二种情况点![]() 在正方形
在正方形![]() 的外部,作图如下,利用正方形和等边三角形的性质及三角形内角和分别求出∠AEB和∠DEC的度数,图(1)是∠BEC=60°﹣(∠AEB+∠DEC),图(2)是∠BEC=360°﹣∠AEB﹣∠AED﹣∠DEC即可求解.
的外部,作图如下,利用正方形和等边三角形的性质及三角形内角和分别求出∠AEB和∠DEC的度数,图(1)是∠BEC=60°﹣(∠AEB+∠DEC),图(2)是∠BEC=360°﹣∠AEB﹣∠AED﹣∠DEC即可求解.
解:如图(1)中,当点E在正方形ABCD外时,
在正方形ABCD中,AB=BC=AD=CD,∠BAD=∠ADC=90°,AB∥CD,
在等边△ADE中,AD=DE=AE,∠ADE=∠AED=∠DAE=60°,
∴AB=AE=CD=DE;
∵AB=AE,
∴∠ABE=∠AEB=![]() (180°-∠BAE)=
(180°-∠BAE)=![]() (180°-90°-60°)=15°;
(180°-90°-60°)=15°;
同理可证∠DCE=∠DEC=15°,
∴在△AED中,
∠BEC=60°-(∠AEB+∠DEC)=60°﹣30°=30°.
∴∠BEC的度数是30°.
如图(2),当点E在正方形ABCD内时,
同理,∠BAD=∠ADC=90°,∠ADE=∠AED=∠DAE=60°,
∴∠BAE=∠CDE=30°;
∵AB=AE,
∴∠ABE=∠AEB=![]() (180°﹣30°)=75°;
(180°﹣30°)=75°;
同理∠DCE=∠DEC=![]() (180°﹣30°)=75°;
(180°﹣30°)=75°;
根据周角的定义,∠BEC=360°﹣∠BEA﹣∠AED﹣∠DEC=360°﹣75°﹣60°﹣75°=150°.
故答案是:30°或150°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
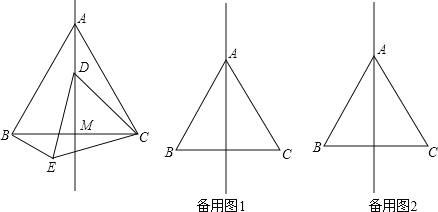
【题目】如图,在等边![]() 中,线段
中,线段![]() 为
为![]() 边上的中线.动点
边上的中线.动点![]() 在直线
在直线![]() 上时,以
上时,以![]() 为一边在
为一边在![]() 的下方作等边
的下方作等边![]() ,连结
,连结![]() .
.
(1)求![]() 的度数;
的度数;
(2)若点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() ;
;
(3)当动点![]() 在直线
在直线![]() 上时,设直线
上时,设直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,试判断
,试判断![]() 是否为定值?并说明理由.
是否为定值?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的A型智能手表,去年销售总额为8000元,今年A型智能手表的售价每只比去年降了60元,若售出的数量与去年相同,销售总额将比去年减少25%.
(1)请问今年A型智能手表每只售价多少元?
(2)今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价与销售价格如下表,若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
A型智能手表 | B型智能手表 | |
进价 | 130元/只 | 150元/只 |
售价 | 今年的售价 | 230元/只 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在矩形![]() 中,
中,![]() 的平分线DE交BC边于点E,点P在线段DE上(其中EP<PD).
的平分线DE交BC边于点E,点P在线段DE上(其中EP<PD).
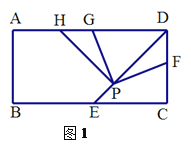
(1)如图1,若点F在CD边上(不与点C,D重合),将![]() 绕点P逆时针旋转90°后,角的两边PD、PF分别交AD边于点H、G.
绕点P逆时针旋转90°后,角的两边PD、PF分别交AD边于点H、G.
①求证:![]() ;
;
②探究:![]() 、
、![]() 、
、![]() 之间有怎样的数量关系,并证明你的结论;
之间有怎样的数量关系,并证明你的结论;
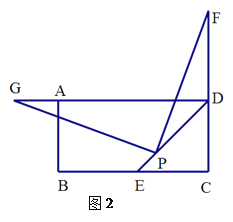
(2)拓展:如图2,若点F在CD的延长线上,过点P作![]() ,交射线DA于点G.你认为(2)中DF、DG、DP之间的数量关系是否仍然成立?若成立,给出证明,若不成立,请写出它们所满足的数量关系式,并说明理由.
,交射线DA于点G.你认为(2)中DF、DG、DP之间的数量关系是否仍然成立?若成立,给出证明,若不成立,请写出它们所满足的数量关系式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() 是边
是边![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 重合),连接
重合),连接![]() .
.
(感知)如图1,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .易证
.易证![]() .(不需要证明)
.(不需要证明)

(探究)如图2,取![]() 的中点
的中点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)连接![]() .若
.若![]() ,则
,则![]() 的长为___________.
的长为___________.

(应用)如图3,取![]() 的中点
的中点![]() ,连接
,连接![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,则四边形
,则四边形![]() 的面积为______.
的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于G,H,试判断下列结论:①△ABE≌△CDF;②AG=GH=HC;③2EG=BG;④S△ABG:S四边形GHDE=2:3,其中正确的结论是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°.

(1)连接AD,根据 易证△ACD≌△ ;
(2)如图2,若E是AC上一点,F是AB延长线上一点,且CE=BF,求证:DE=DF;
(3)如图3,在(2)的条件下,若G在AB上且∠EDG=60°,试猜想CE、EG、BG之间的数量关系并证明所归纳结论;
(4)若题中条件“∠CAB=60°且∠CDB=120°”改为“∠CAB=α,∠CDB=180°﹣α”,G在AB上,∠EDG满足什么条件时,(3)中结论仍然成立?(只写结果不要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,BD,CE分别是两腰上的中线.
(1)求证:BD=CE;
(2)设BD与CE相交于点O,点M,N分别为线段BO和CO的中点,当△ABC的重心到顶点A的距离与底边长相等时,判断四边形DEMN的形状,无需说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com