
【题目】如图,在Rt△ABC中,∠C=90°,CD⊥AB,BE平分∠ABC交CD于F,EH⊥CD于H,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若F为BE中点,则AD=3BD,其中正确的结论有( )
;④若F为BE中点,则AD=3BD,其中正确的结论有( )

A.1个B.2个C.3个D.4个
【答案】D
【解析】
①证明△ACD∽△CBD即可作出判断;
②根据勾股定理即可得解;
③作EM⊥AB,可证△BCE≌△BEM,从而得到![]() 为定值,依此即可作出判断;
为定值,依此即可作出判断;
④若F为BE中点,则CF=EF=BF,可得∠BCD=∠CBF=∠DBF=30°,再根据含30°的直角三角形的性质即可作出判断.
∵CD⊥AB,
∴∠CDA=∠CDB,∠A+∠ACD=90°, ∠CBD+∠BCD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∴∠A=∠BCD
∴△ACD∽△CBD
∴![]()
∴![]()
故①正确;
∵AC2-AD2=BC2-BD2=CD2,
∴AC2+BD2=BC2+AD2,
故②正确;
作EM⊥AB,则BD+EH=BM,
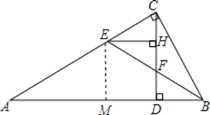
∵BE平分∠ABC,△BCE≌△BEM,
∴BC=BM=BD+EH,
∴![]() =1,故③正确;
=1,故③正确;
∵F为BE中点,
∴BF=EF,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∴∠BFD=90°-∠DBF,
∴∠CFE=90°-∠DBF,
又∠CEF=∠A+∠ABE=90°-∠ABC+∠ABE=90°-∠ABE,
∴∠CFE=∠CEF
∴CE=CF
∵F为BE中点
∴CF=CE
∴CF=EF=BF,
∴∠BCD=∠CBF=∠DBF=30°,∠A=30°,
∴AB=2BC=4BD,
∴AD=3BD,故④正确.
∴正确的结论有4个.
故选D.


科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b和x轴上,已知点B1(1,1),B2(3,2),则B4的坐标_____,Bn的坐标_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
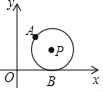
【题目】如图,在平面直角坐标系xoy中,已知圆心为P(x,y)的动圆经过点A(1,2),且与x轴相切于点B.
(1)当x=0时,求⊙P的半径;
(2)请直接写出y与x之间的函数关系式,并求出y的最小值;
(3)在⊙P运动过程中,是否存在某一位置,使得⊙P与x轴、y轴都相切?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
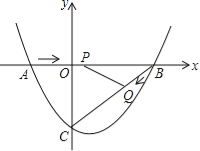
【题目】如图,在平面直角坐标系中,抛物线经过点A(-3,0)、B(2,0)、C(0,4).
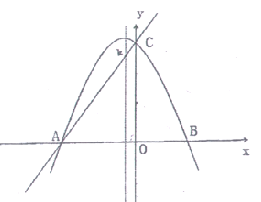
(1)求抛物线的解析式;
(2)在y轴上找一点D,使得△BOD与△AOC相似,请直接写出符合条件的点D的坐标;
(3)若AC与抛物线的对称轴交于点E,以A为圆心,AE长为半径作圆,⊙A与y轴的位置关系如何?请说明理由.
(4)过点E作⊙A的切线EG,交x轴于点G,请求出直线EG的解析式及G点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若抛物线![]() 顶点A的横坐标是
顶点A的横坐标是![]() ,且与y轴交于点
,且与y轴交于点![]() ,点P为抛物线上一点.
,点P为抛物线上一点.
![]() 求抛物线的表达式;
求抛物线的表达式;
![]() 若将抛物线
若将抛物线![]() 向下平移4个单位,点P平移后的对应点为
向下平移4个单位,点P平移后的对应点为![]() 如果
如果![]() ,求点Q的坐标.
,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=4,将矩形ABCD折叠,使得顶点B落在边上的P点处.
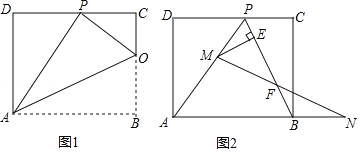
(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1:4,求边AB的长;
(3)如图2,在(1)(2)的条件下,擦去折痕AO线段OP,连结BP,动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
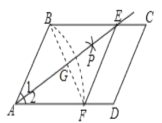
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B. F为圆心,大于![]() BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,AG=2
BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,AG=2![]() ,则四边形ABEF的面积是( )
,则四边形ABEF的面积是( )
A.8![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市实施产业精准扶贫,帮助贫困户承包荒山种植某品种蜜柚.已知该蜜柚的成本价为6元/千克,到了收获季节投入市场销售时,调查市场行情后,发现该蜜柚不会亏本,且每天的销售量y(千克)与销售单价x(元)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某村农户今年共采摘蜜柚12000千克,若该品种蜜柚的保质期为50天,按照(2)的销售方式,能否在保质期内全部销售完这批蜜柚?若能,请说明理由;若不能,应定销售价为多少元时,既能销售完又能获得最大利润?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com