
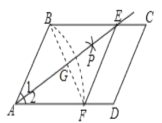
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B. F为圆心,大于![]() BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,AG=2
BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,AG=2![]() ,则四边形ABEF的面积是( )
,则四边形ABEF的面积是( )
A.8![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
由作法得AE平分∠BAD,AB=AF,所以∠1=∠2,再证明AF=BE,则可判断四边形AFEB为平行四边形,于是利用AB=AF可判断四边形ABEF是菱形;根据菱形的性质得BF⊥AE,AG=EG,求出BF和AE的长,即可得出结果.
由作法得AE平分∠BAD,AB=AF,
则∠1=∠2,
∵四边形ABCD为平行四边形,
∴BE∥AF,∠BAF=∠C=60°,
∴∠2=∠BEA,
∴∠1=∠BEA=30°,
∴BA=BE,
∴AF=BE,
∴四边形AFEB为平行四边形,△ABF是等边三角形,而AB=AF,
∴四边形ABEF是菱形;
∴BF⊥AE,AG=EG,
∵四边形ABEF的周长为16,
∴AF=BF=AB=4,
在Rt△ABG中,∠1=30°,
∵AG=2![]() ,
,
∴AE=2AG=4![]() ,
,
∴菱形ABEF的面积=![]() BF×AE=
BF×AE=![]() ×4×4
×4×4![]() =8
=8![]() ;
;
故答案为:A.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,CD⊥AB,BE平分∠ABC交CD于F,EH⊥CD于H,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若F为BE中点,则AD=3BD,其中正确的结论有( )
;④若F为BE中点,则AD=3BD,其中正确的结论有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠A=∠B=30°.
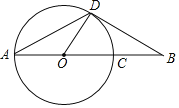
(1)求证:BD是⊙O的切线.
(2)若OA=5,求OA、OD与AD围成的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、C为半径是3的圆周上两点,点B为弧AC的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P为∠MON平分线OC上一点,以P为顶点的∠APB两边分别与射线OM和ON交于A. B两点,如果∠APB在绕点P旋转时始终满足OAOB=OP![]() ,我们就把∠APB叫做∠MON的关联角.
,我们就把∠APB叫做∠MON的关联角.
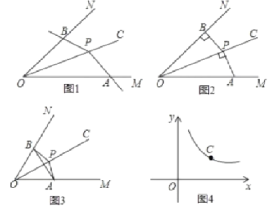
(1)如图2,P为∠MON平分线OC上一点,过P作PB⊥ON于B,AP⊥OC于P,那么∠APB___∠MON的关联角(填“是”或“不是”).
(2)①如图3,如果∠MON=60°,OP=2,∠APB是∠MON的关联角,连接AB,求△AOB的面积和∠APB的度数;
②如果∠MON=α°(0°<α°<90°),OP=m,∠APB是∠MON的关联角,直接用含有α和m的代数式表示△AOB的面积。
(3)如图4,点C是函数y=![]() (x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标。
(x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是1,则数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数是_____,方差是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣![]() x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是( )
x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是( )
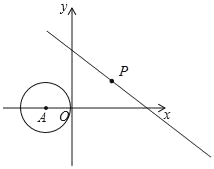
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,与x轴相交于A、B两点(点A在点B的右侧),点A的坐标为(m,0),且AB=4.
(1)填空:点B的坐标为 (用含m的代数式表示);
(2)把射线AB绕点A按顺时针方向旋转135°与抛物线交于点P,△ABP的面积为8:
①求抛物线的解析式(用含m的代数式表示);
②当0≤x≤1,抛物线上的点到x轴距离的最大值为![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com