
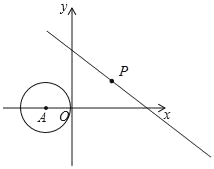
【题目】如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣![]() x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是( )
x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
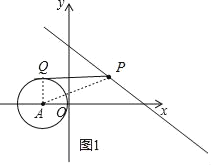
如图1,连接AP、AQ,根据切线的性质得AQ⊥PQ,则利用勾股定理得到PQ=![]() ,则当AP最小时,PQ最小,如图2,直线y=-
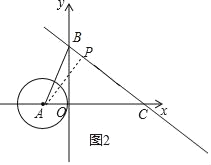
,则当AP最小时,PQ最小,如图2,直线y=-![]() x+3与y轴交于B,与x轴交于点C,则B(0,3),C(4,0),BC=5,利用垂线段最短得到当AP⊥BC于P时,AP最小,利用面积法可计算出AP=3,从而得到PQ的最小值.
x+3与y轴交于B,与x轴交于点C,则B(0,3),C(4,0),BC=5,利用垂线段最短得到当AP⊥BC于P时,AP最小,利用面积法可计算出AP=3,从而得到PQ的最小值.
如图1,连接AP、AQ,
∵PQ为切线,
∴AQ⊥PQ,
在Rt△APQ中,PQ=![]() =
=![]() ,
,
当AP最小时,PQ最小,
如图2,直线y=﹣![]() x+3与y轴交于B,与x轴交于点C,则B(0,3),C(4,0),
x+3与y轴交于B,与x轴交于点C,则B(0,3),C(4,0),
∴BC=![]() =5,
=5,
当AP⊥BC于P时,AP最小,
∵![]() APBC=
APBC=![]() BOAC,
BOAC,
∴AP=![]() =3,
=3,
∴PQ的最小值为![]() =2
=2![]() .
.
故选C.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线经过点A(-3,0)、B(2,0)、C(0,4).
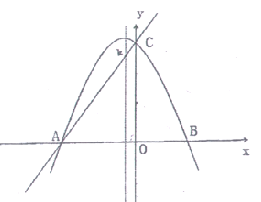
(1)求抛物线的解析式;
(2)在y轴上找一点D,使得△BOD与△AOC相似,请直接写出符合条件的点D的坐标;
(3)若AC与抛物线的对称轴交于点E,以A为圆心,AE长为半径作圆,⊙A与y轴的位置关系如何?请说明理由.
(4)过点E作⊙A的切线EG,交x轴于点G,请求出直线EG的解析式及G点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
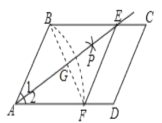
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B. F为圆心,大于![]() BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,AG=2
BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,AG=2![]() ,则四边形ABEF的面积是( )
,则四边形ABEF的面积是( )
A.8![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点

(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= _时,四边形MENF是正方形(只写结论,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在元旦期间,某商场计划购进甲、乙两种商品.
(1)已知甲、乙两种商品的进价分别为30元,70元,该商场购进甲、乙两种商品共50件需要2300元,则该商场购进甲、乙两种商品各多少件?
(2)该商场共投入9500元资金购进这两种商品若干件,这两种商品的进价和售价如表所示:
甲 | 乙 | |
进价(元/件) | 30 | 70 |
售价(元/件) | 50 | 100 |
若全部销售完后可获利5000元(利润=(售价﹣进价)×销量),则该商场购进甲、乙两种商品各多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使得函数值为0的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0可得x=1,我们说1是函数y=x﹣1的零点.已知函数y=x2﹣2mx﹣2(m+3)(m为常数)
(1)当m=0时,求该函数的零点.
(2)证明:无论m取何值,该函数总有两个零点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市实施产业精准扶贫,帮助贫困户承包荒山种植某品种蜜柚.已知该蜜柚的成本价为6元/千克,到了收获季节投入市场销售时,调查市场行情后,发现该蜜柚不会亏本,且每天的销售量y(千克)与销售单价x(元)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某村农户今年共采摘蜜柚12000千克,若该品种蜜柚的保质期为50天,按照(2)的销售方式,能否在保质期内全部销售完这批蜜柚?若能,请说明理由;若不能,应定销售价为多少元时,既能销售完又能获得最大利润?

查看答案和解析>>
科目:初中数学 来源: 题型:
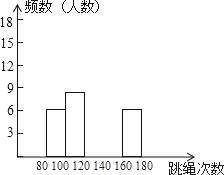
【题目】为了进一步了解八年级学生的身体素质情况,体育老师以八年级(1)班50位学生为样本进行了一分钟跳绳次数测试.根据测试结果,绘制出部分频数分布表和部分频数分布直方图.
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a= ;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)已知该校八年级共有学生800,请你估计一分钟跳绳次数不低于120次的八年级学生大约多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com