
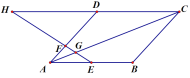
【题目】如图:平行四边形ABCD中,E为AB中点,![]() ,连E、F交AC于G,则AG:GC=______________;
,连E、F交AC于G,则AG:GC=______________;
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠A=∠B=30°.
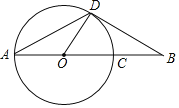
(1)求证:BD是⊙O的切线.
(2)若OA=5,求OA、OD与AD围成的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
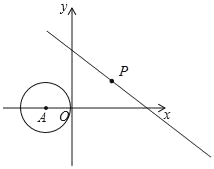
【题目】如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣![]() x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是( )
x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )
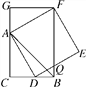
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求![]() 的值.
的值.
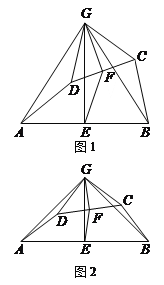
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知梯形![]() 中,
中,![]() ∥
∥![]() ,且
,且![]() ,
,![]() ,
,![]() 。
。
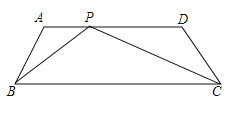
⑴如图,P为![]() 上的一点,满足∠BPC=∠A,求AP的长;
上的一点,满足∠BPC=∠A,求AP的长;
⑵如果点P在![]() 边上移动(点P与点
边上移动(点P与点![]() 不重合),且满足∠BPE=∠A,
不重合),且满足∠BPE=∠A,![]() 交直线
交直线![]() 于点E,同时交直线DC于点
于点E,同时交直线DC于点![]() 。
。
①当点![]() 在线段DC的延长线上时,设
在线段DC的延长线上时,设![]() ,CQ=y,求
,CQ=y,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②写CE=1时,写出AP的长(不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,与x轴相交于A、B两点(点A在点B的右侧),点A的坐标为(m,0),且AB=4.
(1)填空:点B的坐标为 (用含m的代数式表示);
(2)把射线AB绕点A按顺时针方向旋转135°与抛物线交于点P,△ABP的面积为8:
①求抛物线的解析式(用含m的代数式表示);
②当0≤x≤1,抛物线上的点到x轴距离的最大值为![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组同学借助无人机航拍测量某公园内一座古塔高度.如图,无人机在距离地面168米的A处,测得该塔底端点B的俯角为40°,然后向古塔方向沿水平面飞行50秒到达点C处,此时测得该塔顶端点D的俯角为60°.已知无人机的飞行速度为3米/秒,则这座古塔的高度约为_____米(参考计算:sin40°≈064.cos40°≈077.tan40°≈0.84.![]() ≈1.41.
≈1.41.![]() 1.73.结果精确到0.1米)
1.73.结果精确到0.1米)
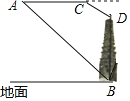
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com