
����Ŀ����֪����ABCD��һ����AD��4��������ABCD�۵���ʹ�ö���B���ڱ��ϵ�P�㴦��
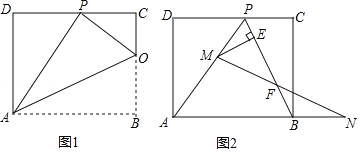
��1����ͼ1����֪�ۺ����BC���ڵ�O������AP��OP��OA����֤����OCP�ס�PDA��
��2������OCP����PDA�������Ϊ1��4�����AB�ij���
��3����ͼ2���ڣ�1����2���������£���ȥ�ۺ�AO�߶�OP������BP������M���߶�AP�ϣ���M���P��A���غϣ�������N���߶�AB���ӳ����ϣ���BN��PM������MN��PB�ڵ�F����ME��BP�ڵ�E�����ʵ���M��N���ƶ������У��߶�EF�ij����Ƿ����仯�����仯��˵�����ɣ������䣬����߶�EF�ij��ȣ�
���𰸡���1������������2��AB��5����3��EF�ij��Ȳ��䣬EF��![]() ��
��
��������
��1�������۵������ʵõ���APO=��B=90�㣬�������������ε��ж�����֤����OCP�ס�PDA��
��2���������������ε�����ȵ������Ʊȵ�ƽ�����
��3����MQ��AB��PB��Q�����ݵ��������ε����ʺ����������ε����ʵõ�EF=![]() PB�����ݹ��ɶ������PB�����㼴�ɣ�
PB�����ݹ��ɶ������PB�����㼴�ɣ�
��1�����ı���ABCD�Ǿ��Σ�
��AD��BC��DC��AB����DAB����B����C����D��90�㣮
���۵��ɵã�AP��AB��PO��BO����PAO����BAO����APO����B��
���APO��90�㣮
���APD��90�㩁��CPO����POC��
�ߡ�D����C����APD����POC��
���OCP�ס�PDA��
��2���ߡ�OCP�ס�PDA�ҡ�OCP���PDA�������Ϊ1��4
��![]() ,
,
��DA��2CP
��AD��4��
��CP��2
��AB��x����AP��CD��x��DP��x��2��
��Rt��ADP��
�ߡ�D��90�㣬AD��4��DP��x��2��AP��x
��x2����x��2��2+42
��ã�x��5
��AB��5
��3��EF�ij��Ȳ��䣮
��ͼ2����MQ��AB��PB��Q��
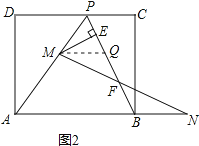
���MQP����ABP��
���۵������ʿ�֪����APB����ABP��
���MQP����APB��
��MP��MQ����BN��PM��
��MQ��BN��
��MQ��AB��
��![]() ��
��
��QF��FB��
��MP��MQ��ME��BP��
��PE��QE��
��EF��![]() PB��
PB��
�ɣ�2���ã�PC��2��BC��4��
��PB��![]() ��
��![]() ��
��
��EF��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪ���Σ���E�DZ�BC���е㣬AF��ED��AE��DF
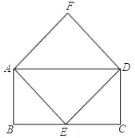
��1����֤���ı���AEDFΪ���Σ�
��2����̽������AB��BC���� ������AEDFΪ�����Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ķ�չ��ͨ��������Ȧ�����Լ�ÿ�����ߵIJ����Ѿ���Ϊһ��ʱ�У�������������С��Ϊ���˽����ĺ��ѵ��˶�����������ȡ�˲��ֺ��ѽ��е��飬������6��1���������ߵ������Ϊ�ĸ����A��0��5000������˵������0��5000����ʾ���ڵ���0��С�ڵ���5000����ͬ����B��5001��10000������C��10001��15000������D��15000�����ϣ���ͳ�ƽ����ͼ��ʾ��

������ͳ�ƽ���ش��������⣺
��1�����ε����У�һ���������� ��λ���ѣ�
��2����֪A�����������D�����������5����
���벹ȫ����ͼ��
������ͼ�У���A����Ӧ���ε�Բ�Ľ�Ϊ�� ���ȣ�
����С��������Ȧ���к���150�ˣ�����ݵ������ݹ��ƴ�Լ�ж���λ����6��1���������ߵIJ�������10000����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90����CD��AB��BEƽ�֡�ABC��CD��F��EH��CD��H�������н��ۣ���![]() ����
����![]() ����
����![]() ������FΪBE�е㣬��AD=3BD��������ȷ�Ľ�����( )
������FΪBE�е㣬��AD=3BD��������ȷ�Ľ�����( )

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
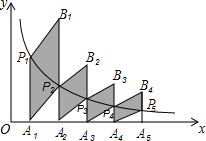
����Ŀ����ͼ���ֱ������������![]() ͼ���ϵĵ�P1(1��y1)��P2(2��y2)������Pn(n��Pn)������x��Ĵ��ߣ�����ֱ�ΪA1��A2������An ��������A1P2��A2P3������An��1Pn����������A1P1��A1P2Ϊһ���ڱ�һ��ƽ���ı���A1P1B1P2����A2P2��A2P3Ϊһ���ڱ�һ��ƽ���ı���A2P2B2P3���������ƣ����Bn����������______________��(����ú�n����ʽ��ʾ)
ͼ���ϵĵ�P1(1��y1)��P2(2��y2)������Pn(n��Pn)������x��Ĵ��ߣ�����ֱ�ΪA1��A2������An ��������A1P2��A2P3������An��1Pn����������A1P1��A1P2Ϊһ���ڱ�һ��ƽ���ı���A1P1B1P2����A2P2��A2P3Ϊһ���ڱ�һ��ƽ���ı���A2P2B2P3���������ƣ����Bn����������______________��(����ú�n����ʽ��ʾ)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�AB����Բ��O������O�ڵ�A��C����DΪ��O��һ�㣬����AD��OD��BD����A����B��30�㣮
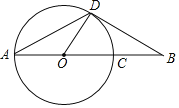
��1����֤��BD�ǡ�O�����ߣ�
��2����OA��5����OA��OD��ADΧ�ɵ����ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��CΪ�뾶��3��Բ�������㣬��BΪ��AC���е㣬���߶�BA��BCΪ�ڱ�������ABCD������Dǡ�ڸ�Բֱ�������ȷֵ��ϣ�������εı߳�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ������x1��x2��x3��x4��x5��ƽ������2��������1��������3x1��2��3x2��2��3x3��2��3x4��2��3x5��2��ƽ������_____��������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
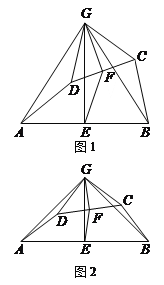
����Ŀ����ͼ1�����ı���ABCD�У���E��F�ֱ���AB��CD���е㣬����E��AB�Ĵ��ߣ�����F��CD�Ĵ��ߣ������߽��ڵ�G������AG��BG��CG��DG������AGD����BGC��
��1����֤��AD��BC��
��2����֤����AGD�ס�EGF��
��3����ͼ2����AD��BC����ֱ���ഹֱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com