
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).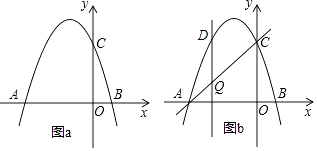
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4S△BOC , 求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
【答案】
(1)解:把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得
![]() ,
,
解得 ![]() .
.
故该抛物线的解析式为:y=﹣x2﹣2x+3.
(2)解:由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).
∵S△AOP=4S△BOC,
∴ ![]() ×3×|﹣x2﹣2x+3|=4×
×3×|﹣x2﹣2x+3|=4× ![]() ×1×3.
×1×3.
整理,得(x+1)2=0或x2+2x﹣7=0,
解得x=﹣1或x=﹣1±2 ![]() .
.
则符合条件的点P的坐标为:(﹣1,4)或(﹣1+2 ![]() ,﹣4)或(﹣1﹣2
,﹣4)或(﹣1﹣2 ![]() ,﹣4)
,﹣4)
(3)解:设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,3)代入,
得 ![]() ,
,
解得 ![]() .
.
即直线AC的解析式为y=x+3.
设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),
QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+ ![]() )2+
)2+ ![]() ,
,
∴当x=﹣ ![]() 时,QD有最大值
时,QD有最大值 ![]()
【解析】(1)利用待定系数法,把点A、C的坐标分别代入函数解析式,列出方程组,求解即可求出抛物线的解析式。
(2)设P点坐标为(x,-x2-2x+3),根据S△AOP=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;
(3)先运用待定系数法求出直线AC的解析式,再设Q点坐标为(x,x+3),则D点坐标为(x,x2+2x-3),然后求出QD与x的函数解析式,求出其顶点坐标,即可求出线段QD长度的最大值。
【考点精析】通过灵活运用公式法和确定一次函数的表达式,掌握要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中。

(1)请写出△ABC各点的坐标;
(2)求出△ABC的面积S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1,并写出△A1B1C1的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
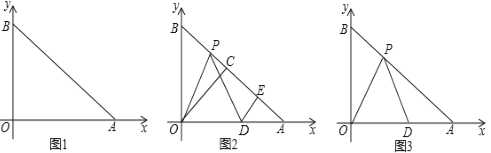
【题目】已知,在平面直角坐标系中,A(a,0)、B(0,b),a、b满足![]() +|a3
+|a3![]() |=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
|=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
(1)求∠OAB的度数;
(2)设AB=6,当点P运动时,PE的值是否变化?若变化,说明理由;若不变,请求PE的值;
(3)设AB=6,若∠OPD=45°,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号min{a,b,c}表示a、b、c三个数中的最小值,如min{1,﹣2,3}=﹣2,min{0,5,5}=0.
(1)根据题意填空:min![]() = ;
= ;
(2)试求函数y=min{2,x+1,﹣3x+11}的解析式;
(3)关于x的方程﹣x+m=min{2,x+1,﹣3x+11}有解,试求常数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
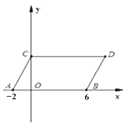
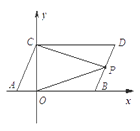
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-2,0),(6,0),现同时将点A,B分别向上平移4个单位,再向右平移2个单位,分别得到点A,B的对应点C、D,连接AC、BD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC
(2)在y轴上是否存在一点P,连接PA、PB,使S△PAB=S四边形ABDC,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)给出下列结论:①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() ,点
,点![]() 在射线
在射线![]() 上运动(
上运动(![]() 点与
点与![]() 三点不重合),设
三点不重合),设![]() ,
,![]() ,
,![]() .
.

(1)如果点![]() 在
在![]() 两点之间运动时,
两点之间运动时,![]() 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;
(2)如果点![]() 在
在![]() 两点之外运动时,
两点之外运动时,![]() 之间有何数量关系?(只需写出结论,不必说明理由)
之间有何数量关系?(只需写出结论,不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条高AD,BE交于点F,∠ABC=45°,∠BAC=60°.
(1)求证:DF=DC;
(2)连接CF,求证:AB=AC+CF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,已知AD∥BC,AB⊥BC,点E,F在边AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣ ![]() ,FC=2
,FC=2 ![]() .
.
(1)BC= ;
(2)求点D到BC的距离;
(3)求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=5,AB=3.
(1)利用尺规在AC上找到一点D,使得DA=DC(保留作图痕迹,不写作法).
(2)连接DB,若DA=DC=DB,试判断△ABC的形状,说明理由,并求出△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com