
【题目】如图,在四边形ABCD中,已知AD∥BC,AB⊥BC,点E,F在边AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣ ![]() ,FC=2
,FC=2 ![]() .
.
(1)BC= ;
(2)求点D到BC的距离;
(3)求DC的长.
【答案】
(1)3
(2)解:过点D作DG⊥BC于点G,
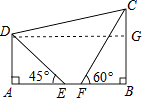
∵AD∥BC,AB⊥BC,
∴DG=AB,DA⊥AB,
∵FC=2 ![]() ,∠BFC=60°,
,∠BFC=60°,
∴BF=FCcos60°= ![]() ,
,
∴DG=AB=AE+EF+BF=2+2﹣ ![]() +
+ ![]() =4
=4
(3)解:∵DA⊥AB,∠AED=45°,
∴AD=AE=2,
∵DG⊥BC,AB⊥BC,
∴DG∥AB,
∵AD∥BC,
∴四边形ABGD是矩形,
∴BG=AD=2,
∴CG=BC﹣BG=3﹣2=1,
∴在Rt△DCG中,CD= ![]() =
= ![]()
【解析】解:(1)∵AB⊥BC,
∴∠B=90°,
∵FC=2 ![]() ,∠BFC=60°,
,∠BFC=60°,
∴BC=FCsin60°=2 ![]() ×
× ![]() =3;
=3;
所以答案是:3.
【考点精析】关于本题考查的勾股定理的概念和解直角三角形,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠DEA=( )
A.40°
B.110°
C.70°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).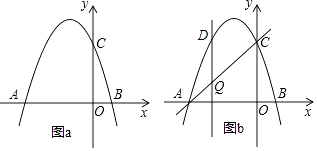
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4S△BOC , 求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有个点![]() ,点
,点![]() 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点![]() ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点![]() ,第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第200次跳动至点
,第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第200次跳动至点![]() 的坐标是( )
的坐标是( )

A. (51,100)B. (50,100)C. (-50,100)D. (-51,100)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列结论:
①OA=OD;
②AD⊥EF;
③AE+DF=AF+DE;
④当∠BAC=90°时,四边形AEDF是正方形.
其中一定正确的是( )
A.①②③
B.②③④
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班要从甲、乙两名同学中选拔出一人,代表班级参加学校的一分钟踢毽子体能素质比赛,在一段时间内的相同条件下,甲、乙两人进行了六场一分钟踢毽子的选拔测试,根据他们的成绩绘制出如图的统计表和不完整的折线统计图.
甲、乙两人选拔测试成绩统计表
甲成绩 | 乙成绩 | |
第1场 | 87 | 87 |
第2场 | 94 | 98 |
第3场 | 91 | 87 |
第4场 | 85 | 89 |
第5场 | 91 | 100 |
第6场 | 92 | 85 |
中位数 | 91 | n |
平均数 | m | 91 |
并计算出乙同学六场选拔测试成绩的方差:
S乙2= ![]() =
= ![]()
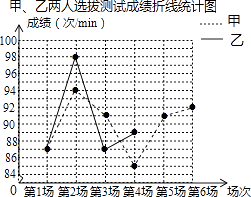
(1)m= , n= , 并补全全图中甲、乙两人选拔测试成绩折线统计图;
(2)求甲同学六场选拔测试成绩的方差S甲2;
(3)分别从平均数、中位数和方差的角度分析比较甲、乙二人的成绩各有什么特点?
(4)经查阅该校以往本项比赛的资料可知,①成绩若达到90次/min,就有可能夺得冠军,你认为选谁参赛更有把握夺冠?为什么?
②该项成绩的最好记录是95次/min,就有可能夺得冠军,你认为选谁参赛更有把握夺冠?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,BC=3,AB=8,E、F为AB、CD边上的中点,如图1,A在原点处,点B在y轴正半轴上,点C在第一象限,若点A从原点出发,沿x轴向右以每秒1个单位长度的速度运动,则点B随之沿y轴下滑,并带动矩形ABCD在平面上滑动,如图2,设运动时间表示为t秒,当B到达原点时停止运动.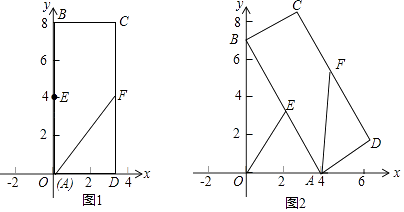
(1)当t=0时,求点F的坐标及FA的长度;
(2)当t=4时,求OE的长及∠BAO的大小;
(3)求从t=0到t=4这一时段点E运动路线的长;
(4)当以点F为圆心,FA为半径的圆与坐标轴相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“百变魔方”社团准备购买![]() 、
、![]() 两种魔方,已知购买
两种魔方,已知购买![]() 个
个![]() 种魔方和
种魔方和![]() 个
个![]() 种魔方共需
种魔方共需![]() 元,又知购买
元,又知购买![]() 个
个![]() 种魔方所需款数和购买
种魔方所需款数和购买![]() 个
个![]() 种魔方所需款数相同.
种魔方所需款数相同.
(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买![]() 、
、![]() 两种魔方共
两种魔方共![]() 个.某商店有两种优惠活动,如图所示。请根据以上信息,如何购买可以使两种优惠方案一致.
个.某商店有两种优惠活动,如图所示。请根据以上信息,如何购买可以使两种优惠方案一致.
⑶当购买![]() 种魔方
种魔方![]() 个时该如何花费才能使得所花钱数最少.
个时该如何花费才能使得所花钱数最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在ΔABC外的点![]() 处,若∠1=20°,则∠2的度数为( )
处,若∠1=20°,则∠2的度数为( )

A. 80°B. 90°
C. 100°D. 110°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com