
【题目】如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列结论:
①OA=OD;
②AD⊥EF;
③AE+DF=AF+DE;
④当∠BAC=90°时,四边形AEDF是正方形.
其中一定正确的是( )
A.①②③
B.②③④
C.①③④
D.①②③④
【答案】B
【解析】解:如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,
∴①不正确;
∵AD是△ABC的角平分线,
∴∠EAD∠FAD,
在△AED和△AFD中,
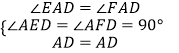 ,
,
∴△AED≌△AFD(AAS),
∴AE=AF,DE=DF,
∴AE+DF=AF+DE,
∴③正确;
在△AEO和△AFO中,
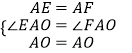 ,
,
∴△AE0≌△AF0(SAS),
∴EO=FO,
又∵AE=AF,
∴AO是EF的中垂线,
∴AD⊥EF,
∴②正确;
∵当∠A=90°时,四边形AEDF的四个角都是直角,
∴四边形AEDF是矩形,
又∵DE=DF,
∴四边形AEDF是正方形,
∴④正确.
综上,可得正确的是:②③④.
所以答案是:B.
【考点精析】掌握线段垂直平分线的判定和角的平分线判定是解答本题的根本,需要知道和一条线段两个端点距离相等的点,在这条线段的垂直平分线上;可以证明三角形内存在一个点,它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点).


科目:初中数学 来源: 题型:
【题目】定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是 , 推断的数学依据是 .
(2)如图②,在△ABC中,∠B=45°,AB= ![]() ,BC=8,AD为边BC的中线,求边BC的中垂距.
,BC=8,AD为边BC的中线,求边BC的中垂距.
(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-2,0),(6,0),现同时将点A,B分别向上平移4个单位,再向右平移2个单位,分别得到点A,B的对应点C、D,连接AC、BD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC
(2)在y轴上是否存在一点P,连接PA、PB,使S△PAB=S四边形ABDC,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)给出下列结论:①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
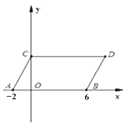
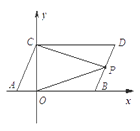
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条高AD,BE交于点F,∠ABC=45°,∠BAC=60°.
(1)求证:DF=DC;
(2)连接CF,求证:AB=AC+CF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H分别是AB,AC,CD,BD的中点,则四边形EFGH的周长是( )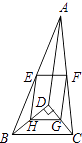
A.7
B.9
C.10
D.11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,已知AD∥BC,AB⊥BC,点E,F在边AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣ ![]() ,FC=2
,FC=2 ![]() .
.
(1)BC= ;
(2)求点D到BC的距离;
(3)求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年国际马拉松赛于承德市举办,起点承德市狮子园,赛道为外环路,终点为奥体中心(赛道基本为直线).在赛道上有A,B两个服务点,现有甲,乙两个服务人员,分别从A,B两个服务点同时出发,沿直线匀速跑向终点C(奥体中心),如图1所示,设甲、乙两人出发xh后,与B点的距离分别为y甲km、y乙km,y甲、y乙与x的函数关系如图2所示.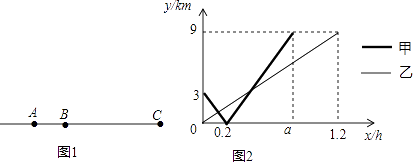
(1)从服务点A到终点C的距离为km,a=h;
(2)求甲乙相遇时x的值;
(3)甲乙两人之间的距离应不超过1km时,称为最佳服务距离,从甲、乙相遇到甲到达终点以前,保持最佳服务距离的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,A(1,3),B(2,1),直角坐标系中存在点C,使得O,A,B,C四点构成平行四边形,则C点的坐标为______________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com