
【题目】定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是 , 推断的数学依据是 .
(2)如图②,在△ABC中,∠B=45°,AB= ![]() ,BC=8,AD为边BC的中线,求边BC的中垂距.
,BC=8,AD为边BC的中线,求边BC的中垂距.
(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.
【答案】
(1)等腰三角形,线段的垂直平分线上的点到两端的距离相等
(2)解:如图②中,作AE⊥BC于E.
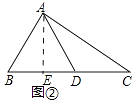
在Rt△ABE中,∵∠AEB=90°,∠B=45°,AB=3 ![]() ,
,
∴AE=BE=3,
∵AD为BC边中线,BC=8,
∴BD=DC=4,
∴DE=BD﹣BE=4﹣3=1,
∴边BC的中垂距为1
(3)解:如图③中,作CH⊥AF于H.
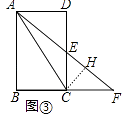
∵四边形ABCD是矩形,
∴∠D=∠EHC=∠ECF=90°,AD∥BF,
∵DE=EC,∠AED=∠CEF,
∴△ADE≌△FCE,
∴AE=EF,
在Rt△ADE中,∵AD=4,DE=3,
∴AE= ![]() =5,
=5,
∵∠D=EHC,∠AED=∠CEH,
∴△ADE∽△CHE,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴EH= ![]() ,
,
∴△ACF中边AF的中垂距为 ![]()
【解析】解:(1)三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是等腰三角形,推断的数学依据是线段的垂直平分线上的点到两端的距离相等.
所以答案是等腰三角形,线段的垂直平分线上的点到两端的距离相等.
【考点精析】关于本题考查的勾股定理的概念和矩形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图1,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.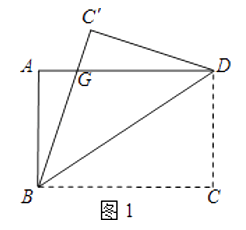
(1)求证:AG=C′G;
(2)如图2,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,求EM的长.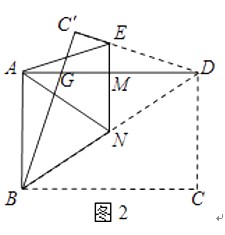
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=9,AC=12.分别以点A和点B为圆心、大于AB一半的长为半径作圆弧,两弧相交于点E和点F,作直线EF交AB于点D,连结CD.则CD的长为 . 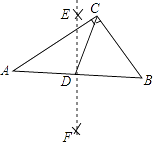
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两条长度均为2的线段![]() 和线段
和线段![]() 互相重合,将
互相重合,将![]() 沿直线
沿直线![]() 向左平移
向左平移![]() 个单位长度,将
个单位长度,将![]() 沿直线
沿直线![]() 向右也平移
向右也平移![]() 个单位长度,当
个单位长度,当![]() 、
、![]() 是线段
是线段![]() 的三等分点时,则
的三等分点时,则![]() 的值为________.
的值为________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,连接
,连接![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
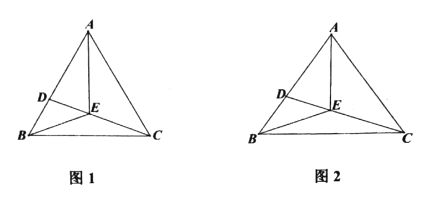
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,在不添加任何辅助线的情况下,请直接写出图中所有底角为
,在不添加任何辅助线的情况下,请直接写出图中所有底角为![]() 的等腰三角形.
的等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠DEA=( )
A.40°
B.110°
C.70°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
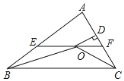
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点O,过O点作
的平分线相交于点O,过O点作![]() 交AB于点E,交AC于点F,过点O作
交AB于点E,交AC于点F,过点O作![]() 于D,下列四个结论.
于D,下列四个结论.
![]()
![]()
![]() 点O到
点O到![]() 各边的距离相等
各边的距离相等![]() 设
设![]() ,
,![]() ,则
,则![]() ,正确的结论有
,正确的结论有![]()
![]() 个.
个.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y= ![]() (x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
(x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
①双曲线的解析式为y= ![]() (x>0);②E点的坐标是(5,8);③sin∠COA=
(x>0);②E点的坐标是(5,8);③sin∠COA= ![]() ;④AC+OB=12
;④AC+OB=12 ![]() .其中正确的结论有( )
.其中正确的结论有( )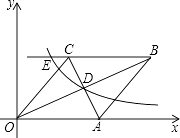
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列结论:
①OA=OD;
②AD⊥EF;
③AE+DF=AF+DE;
④当∠BAC=90°时,四边形AEDF是正方形.
其中一定正确的是( )
A.①②③
B.②③④
C.①③④
D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com