
【题目】已知:![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,连接
,连接![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
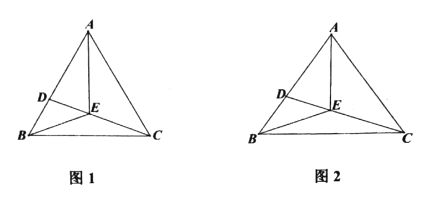
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,在不添加任何辅助线的情况下,请直接写出图中所有底角为
,在不添加任何辅助线的情况下,请直接写出图中所有底角为![]() 的等腰三角形.
的等腰三角形.
【答案】(1)见解析;(2)△ABE,△ACE,△DBE
【解析】
(1)先根据SSS证明△ABE≌△ACE,证得∠DBE=∠ACD,再根据三角形外角的性质,得出∠DBE=∠DEB,即可证出结论.
(2)计算出相关角度,根据等角对等边即可判定
∵AE平分∠BAC ∴∠BAE=∠CAE
∵AB=AC ∠BAE=∠CAE AE=AE
∴△ABE≌△ACE ,∴∠DBE=∠ACD
∵∠ADC=2∠ACD ∴∠ADC=2∠DBE
∵∠ADC=∠DBE+∠DEB ∴∠DBE=∠DEB
∴BD=ED
(2)在![]() 中,∵
中,∵![]() ,
,![]() .
.
∴∠ADC=![]() , ∠ACD=
, ∠ACD=![]() ,由(1)知:∠DBE=∠ACD
,由(1)知:∠DBE=∠ACD
∴∠DBE=∠ACD=![]() , ∴∠DBE=∠DEB=
, ∴∠DBE=∠DEB=![]()
∴△DBE是底角为![]() 的等腰三角形.
的等腰三角形.
∵AE平分∠BAC ∠ADC=![]() ,
,
∴∠BAE=∠CAE![]() DBE=∠DEB
DBE=∠DEB
∴△ABE和△ACE是底角为![]() 的等腰三角形.
的等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=x+m与y= ![]() 在第一象限交于点A,且与x轴交于点C,AB⊥x轴,垂足为B,且S△AOB=1.
在第一象限交于点A,且与x轴交于点C,AB⊥x轴,垂足为B,且S△AOB=1.
(1)求m的值;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)【参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是 , 推断的数学依据是 .
(2)如图②,在△ABC中,∠B=45°,AB= ![]() ,BC=8,AD为边BC的中线,求边BC的中垂距.
,BC=8,AD为边BC的中线,求边BC的中垂距.
(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD交于点O,若增加一个条件,使ABCD成为菱形,下列给出的条件不正确的是( )
A.AB=AD
B.AC⊥BD
C.AC=BD
D.∠BAC=∠DAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在3×3的方格中,A,B,C,D,E,F分别位于格点上,从C,D,E,F四点中任意取一点,与点A,B为顶点作三角形,则所作三角形为等腰三角形的概率是( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H分别是AB,AC,CD,BD的中点,则四边形EFGH的周长是( )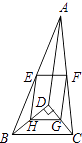
A.7
B.9
C.10
D.11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com