
����Ŀ������ABCD�У�BC=3��AB=8��E��FΪAB��CD���ϵ��е㣬��ͼ1��A��ԭ�㴦����B��y���������ϣ���C�ڵ�һ���ޣ�����A��ԭ���������x��������ÿ��1����λ���ȵ��ٶ��˶������B��֮��y���»�������������ABCD��ƽ���ϻ�������ͼ2�����˶�ʱ���ʾΪt�룬��B����ԭ��ʱֹͣ�˶���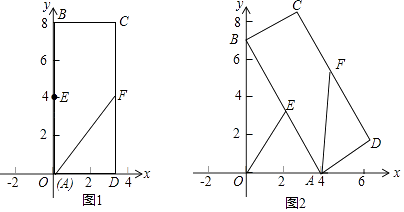
��1����t=0ʱ�����F�����꼰FA�ij��ȣ�
��2����t=4ʱ����OE�ij�����BAO�Ĵ�С��
��3�����t=0��t=4��һʱ�ε�E�˶�·�ߵij���
��4�����Ե�FΪԲ�ģ�FAΪ�뾶��Բ������������ʱ����t��ֵ��
���𰸡�
��1���⣺��t=0ʱ��
��AB=CD=8��FΪCD�е㣬
��DF=4��
��F��3��4����
��AF=5
��2���⣺��t=4ʱ��OA=4��
��Rt��ABO�У�AB=8����AOB=90�㣬��E��AB���е㣬
���ABO=30�㣬OE=4��
���BAO=60��
��3���⣺��t=0��t=4��һʱ�Σ���E�˶�·������OΪԲ�ģ�OEΪ�뾶Բ�Ľ���30���һ�λ���
������OE=OE1=4����E1OE=90�㩁60��=30�㣬��
���E�˶�·�ߵij�Ϊ ![]() =
= ![]() �У�
�У� 
��4���⣺��Rt��ADF�У�FD2+AD2=AF2��
��AF= ![]() =5��
=5��
����AO=t1ʱ����F��x�����У���AΪ�е㣬
��FA��OA��
���OAB+��FAB=90�㣬
�ߡ�FAD+��FAB=90�㣬
���BAO=��FAD��
�ߡ�BOA=��D=90�㣬
��Rt��FAE��Rt��ABO��
�� ![]() ��
��
�� ![]() ��
��
��t1= ![]() ��
��
����AO=t2ʱ����F��y�����У�BΪ�е㣬ͬ���ɵã�t2= ![]() ��
��
�������������Ե�FΪԲ�ģ�FAΪ�뾶��Բ������������ʱ��t��ֵΪ ![]() ��
�� ![]() ��
��
����������1��FΪCD���ϵ��е㣬���DF�ó��������ó���F�����꼴�ɵó�AF��
��2������ֱ�������ε����ʣ�ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬֤�á�AOE�ǵȱ������Σ����ɵó����ۡ�
��3�����жϳ���E�˶���·����һ���������û�����ʽ���ɵó����ۣ�
��4�����������������AO=t1ʱ����F��x�����У���AΪ�е㣻����AO=t2ʱ����F��y�����У�BΪ�е㣬�������������ε����ʽ���������⼴�ɣ�
�����㾫����������Ĺؼ���������ֱ��������б���ϵ����ߵ����֪ʶ������ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬�Լ��Թ��ɶ����ĸ�������⣬�˽�ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵ�У�A��a��0����B��0��b����a��b����![]() +|a3
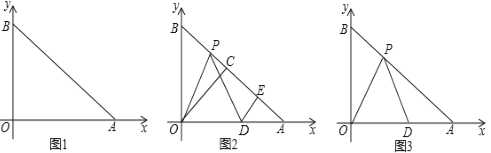
+|a3![]() |��0��CΪAB���е㣬P���߶�AB��һ���㣬D��x����������һ�㣬��PO=PD��DE��AB��E��
|��0��CΪAB���е㣬P���߶�AB��һ���㣬D��x����������һ�㣬��PO=PD��DE��AB��E��
��1������OAB�Ķ�����
��2����AB=6������P�˶�ʱ��PE��ֵ�Ƿ�仯�����仯��˵�����ɣ������䣬����PE��ֵ��
��3����AB=6������OPD=45�������D������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��������AD��BE���ڵ�F����ABC��45������BAC��60����
��1����֤��DF��DC��
��2������CF����֤��AB��AC+CF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���֪AD��BC��AB��BC����E��F�ڱ�AB�ϣ��ҡ�AED=45�㣬��BFC=60�㣬AE=2��EF=2�� ![]() ��FC=2
��FC=2 ![]() ��
��
��1��BC= ��
��2�����D��BC�ľ��룻
��3����DC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016��������������ڳе��оٰ죬���е���ʨ��������Ϊ�·���յ�Ϊ�������ģ���������Ϊֱ�ߣ�������������A��B��������㣬���мף�������������Ա���ֱ��A��B���������ͬʱ��������ֱ�����������յ�C���������ģ�����ͼ1��ʾ����ס������˳���xh����B��ľ���ֱ�Ϊy��km��y��km��y����y����x�ĺ�����ϵ��ͼ2��ʾ��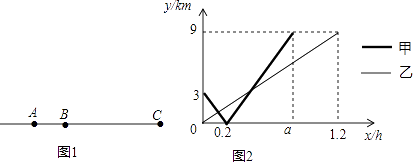
��1���ӷ����A���յ�C�ľ���Ϊkm��a=h��
��2�����������ʱx��ֵ��
��3����������֮��ľ���Ӧ������1kmʱ����Ϊ��ѷ�����룬�Ӽס��������������յ���ǰ��������ѷ�������ʱ���ж��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ�����λͬѧ�ֱ���ȷָ����ijһ��������һ�����ʣ��ף�����ͼ����һ���ޣ��ң�����ͼ���������ޣ�����ÿ��һ�������ڣ�yֵ��xֵ���������С���������ǵ������������������ʽ�����ǣ� ��
A.y=2x
B.y= ![]()
C.y=�� ![]()
D.y=2x2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,OΪ����ԭ��,A(1,3),B(2,1),ֱ������ϵ�д��ڵ�C,ʹ��O,A,B,C�ĵ㹹��ƽ���ı���,��C�������Ϊ______________________________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AC=5��AB=3��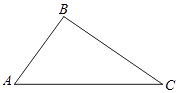
��1�����ó߹���AC���ҵ�һ��D��ʹ��DA=DC��������ͼ�ۼ�����д��������
��2������DB����DA=DC=DB�����жϡ�ABC����״��˵�����ɣ��������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C��90�㣬OΪ��ABC��������ƽ���ߵĽ��㣬OD��BC��OE��AC��OF��AB����D��E��F�ֱ��Ǵ��㣬��AB��10cm��BC��8cm��CA��6cm�����O����AB�ľ���Ϊ(����)
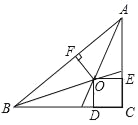
A. 2cmB. 3cmC. 4cmD. 5cm
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com