
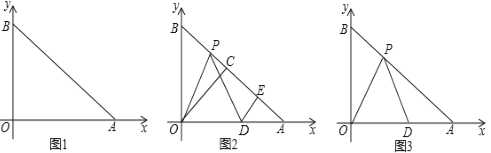
【题目】已知,在平面直角坐标系中,A(a,0)、B(0,b),a、b满足![]() +|a3
+|a3![]() |=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
|=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
(1)求∠OAB的度数;
(2)设AB=6,当点P运动时,PE的值是否变化?若变化,说明理由;若不变,请求PE的值;
(3)设AB=6,若∠OPD=45°,求点D的坐标.
【答案】(1) 45°;(2)PE的值不变,PE=3;(3)D(![]() 6,0).
6,0).
【解析】
试题(1)根据非负数的性质即可求得a,b的值,从而得到△AOB是等腰直角三角形,据此即可求得;
(2)根据等腰三角形的性质以及三角形的外角的性质可以得到∠POC=∠DPE,即可证得△POC≌△DPE,则OC=PE,OC的长度根据等腰直角三角形的性质可以求得;
(3)利用等腰三角形的性质,以及外角的性质证得∠POC=∠DPE,即可证得△POC≌△DPE,根据全等三角形的对应边相等,即可求得OD的长,从而求得D的坐标.
试题解析:(1)根据题意得:
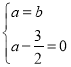 ,
,
解得:a=b=![]() ,
,
∴OA=OB,
又∵∠AOB=90°
∴△AOB为等腰直角三角形,
∴∠OAB=45°.
(2)PE的值不变.理由如下:
∵△AOB为等腰直角三角形,且AC=BC,
∴∠AOC=∠BOC=45°
又∵OC⊥AB于C,
∵PO=PD
∴∠POD=∠PDO
又∵∠POD=45°+∠POC∠PDO=45°+∠DPE,
∴∠POC=∠DPE
在△POC和△DPE中,
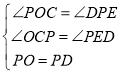
∴△POC≌△DPE,
∴OC=PE
又OC=![]() AB=3
AB=3
∴PE=3;
(3)∵OP=PD,
∴∠POD=∠PDO=![]() ,
,
则∠PDA=180°-∠PDO=180°-67.5°=112.5°,
∵∠POD=∠A+∠APD,
∴∠APD=67.5°-45°=22.5°,
∴∠BPO=180°-∠OPD-∠APD=112.5°,
∴∠PDA=∠BPO
则在△POB和△DPA中,
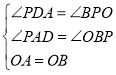 ,
,
∴△POB≌△DPA.
∴PA=OA=![]() ,
,
∴DA=PB=6-![]() ,
,
∴OD=OA-DA=![]() -(6-
-(6-![]() )=
)=![]() -6
-6
∴D(![]() 6,0).
6,0).


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两条长度均为2的线段![]() 和线段
和线段![]() 互相重合,将
互相重合,将![]() 沿直线
沿直线![]() 向左平移
向左平移![]() 个单位长度,将
个单位长度,将![]() 沿直线
沿直线![]() 向右也平移
向右也平移![]() 个单位长度,当
个单位长度,当![]() 、
、![]() 是线段
是线段![]() 的三等分点时,则
的三等分点时,则![]() 的值为________.
的值为________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠DEA=( )
A.40°
B.110°
C.70°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
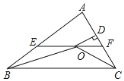
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点O,过O点作
的平分线相交于点O,过O点作![]() 交AB于点E,交AC于点F,过点O作
交AB于点E,交AC于点F,过点O作![]() 于D,下列四个结论.
于D,下列四个结论.
![]()
![]()
![]() 点O到
点O到![]() 各边的距离相等
各边的距离相等![]() 设
设![]() ,
,![]() ,则
,则![]() ,正确的结论有
,正确的结论有![]()
![]() 个.
个.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )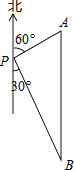
A.60海里
B.45海里
C.20 ![]() 海里
海里
D.30 ![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y= ![]() (x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
(x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
①双曲线的解析式为y= ![]() (x>0);②E点的坐标是(5,8);③sin∠COA=
(x>0);②E点的坐标是(5,8);③sin∠COA= ![]() ;④AC+OB=12
;④AC+OB=12 ![]() .其中正确的结论有( )
.其中正确的结论有( )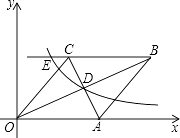
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).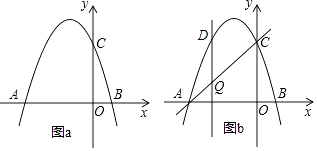
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4S△BOC , 求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,BC=3,AB=8,E、F为AB、CD边上的中点,如图1,A在原点处,点B在y轴正半轴上,点C在第一象限,若点A从原点出发,沿x轴向右以每秒1个单位长度的速度运动,则点B随之沿y轴下滑,并带动矩形ABCD在平面上滑动,如图2,设运动时间表示为t秒,当B到达原点时停止运动.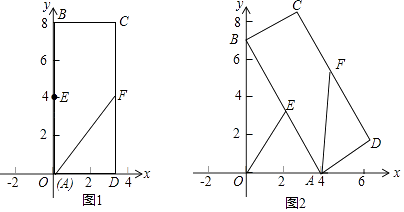
(1)当t=0时,求点F的坐标及FA的长度;
(2)当t=4时,求OE的长及∠BAO的大小;
(3)求从t=0到t=4这一时段点E运动路线的长;
(4)当以点F为圆心,FA为半径的圆与坐标轴相切时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com