
【题目】如图,在△ABC中,AC=5,AB=3.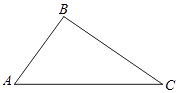
(1)利用尺规在AC上找到一点D,使得DA=DC(保留作图痕迹,不写作法).
(2)连接DB,若DA=DC=DB,试判断△ABC的形状,说明理由,并求出△ABC的面积.
【答案】
(1)解:如图所示:D点即为所求

(2)解:∵DA=DC=DB,
∴∠A=∠ABD,∠C=∠CBD,
∵∠A+∠C+∠ABD+∠CBD=180°,
∴∠A+∠C=90°,
∴△ABC是直角三角形,
∵AC=5,AB=3,
∴BC=4,
∴△ABC的面积为: ![]() ×3×4=6
×3×4=6
【解析】(1)根据已知可知作线段AC的垂直平分线,即可得出AC的中点D。
(2)先由等腰三角形的性质得出∠A=∠ABD,∠C=∠CBD,再由三角形的内角和定理,去证明△ABC是直角三角形,即可求出△ABC的面积。
【考点精析】通过灵活运用三角形的面积和线段垂直平分线的性质,掌握三角形的面积=1/2×底×高;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).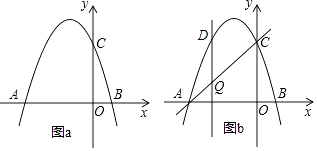
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4S△BOC , 求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,BC=3,AB=8,E、F为AB、CD边上的中点,如图1,A在原点处,点B在y轴正半轴上,点C在第一象限,若点A从原点出发,沿x轴向右以每秒1个单位长度的速度运动,则点B随之沿y轴下滑,并带动矩形ABCD在平面上滑动,如图2,设运动时间表示为t秒,当B到达原点时停止运动.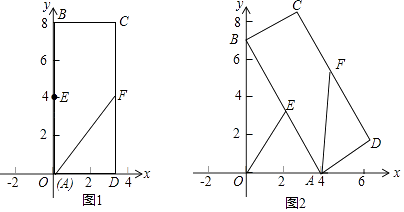
(1)当t=0时,求点F的坐标及FA的长度;
(2)当t=4时,求OE的长及∠BAO的大小;
(3)求从t=0到t=4这一时段点E运动路线的长;
(4)当以点F为圆心,FA为半径的圆与坐标轴相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“百变魔方”社团准备购买![]() 、
、![]() 两种魔方,已知购买
两种魔方,已知购买![]() 个
个![]() 种魔方和
种魔方和![]() 个
个![]() 种魔方共需
种魔方共需![]() 元,又知购买
元,又知购买![]() 个
个![]() 种魔方所需款数和购买
种魔方所需款数和购买![]() 个
个![]() 种魔方所需款数相同.
种魔方所需款数相同.
(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买![]() 、
、![]() 两种魔方共
两种魔方共![]() 个.某商店有两种优惠活动,如图所示。请根据以上信息,如何购买可以使两种优惠方案一致.
个.某商店有两种优惠活动,如图所示。请根据以上信息,如何购买可以使两种优惠方案一致.
⑶当购买![]() 种魔方
种魔方![]() 个时该如何花费才能使得所花钱数最少.
个时该如何花费才能使得所花钱数最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a是一个长为![]() 、宽为
、宽为![]() 的长方形(其中
的长方形(其中![]() >
>![]() ), 沿图中虚线用剪刀均分成四块小长方形, 然后按图
), 沿图中虚线用剪刀均分成四块小长方形, 然后按图![]() 的形状拼成一个正方形,
的形状拼成一个正方形,
(1)①请你用两种不同的方法表示图![]() 中的阴影部分的面积 ; ;
中的阴影部分的面积 ; ;
②请写出代数式:![]() ,
,![]() ,
,![]() 之间的关系: ;
之间的关系: ;
(2)若![]() ,求:
,求:![]() 的值;
的值;
(3)已知![]() ,求:
,求:![]() 的值.
的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+bx﹣ ![]() (a≠0)经过点A(1,0)和B(﹣3,0).
(a≠0)经过点A(1,0)和B(﹣3,0).
(1)求抛物线C1的解析式,并写出其顶点C的坐标.
(2)如图1,把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2 , 此时点A,C分别平移到点D,E处.设点F在抛物线C1上且在x轴的上方,若△DEF是以EF为底的等腰直角三角形,求点F的坐标.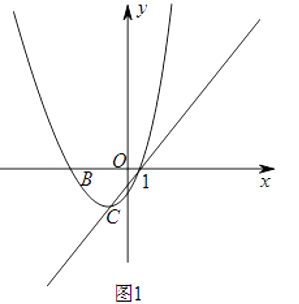
(3)如图2,在(2)的条件下,设点M是线段BC上一动点,EN⊥EM交直线BF于点N,点P为线段MN的中点,当点M从点B向点C运动时:①tan∠ENM的值如何变化?请说明理由;②点M到达点C时,直接写出点P经过的路线长.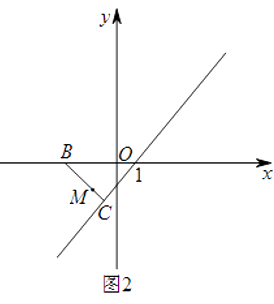
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年怀柔区中考体育加试女子800米耐力测试中,同时起跑的李丽和吴梅所跑的路程![]() 米
米![]() 与所用时间
与所用时间![]() 秒
秒![]() 之间的函数图象分别为线段OA和折线
之间的函数图象分别为线段OA和折线![]() 下列说法正确的是
下列说法正确的是![]()
![]()
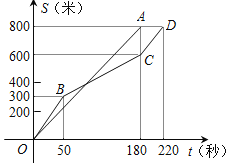
A. 李丽的速度随时间的增大而增大
B. 吴梅的平均速度比李丽的平均速度大
C. 在起跑后180秒时,两人相遇
D. 在起跑后50秒时,吴梅在李丽的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在ΔABC外的点![]() 处,若∠1=20°,则∠2的度数为( )
处,若∠1=20°,则∠2的度数为( )

A. 80°B. 90°
C. 100°D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com