
����Ŀ����֪������C1��y=ax2+bx�� ![]() ��a��0��������A��1��0����B����3��0����
��a��0��������A��1��0����B����3��0����
��1����������C1�Ľ���ʽ����д���䶥��C�����꣮
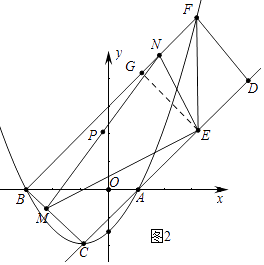
��2����ͼ1����������C1����ֱ��AC����ƽ�Ƶ�ij��ʱ�õ�������C2 �� ��ʱ��A��C�ֱ�ƽ�Ƶ���D��E�������F��������C1������x����Ϸ�������DEF����EFΪ�ĵ���ֱ�������Σ����F�����꣮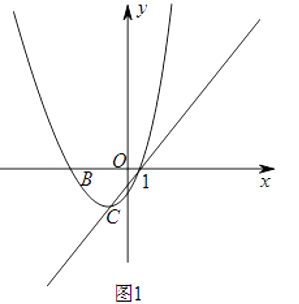
��3����ͼ2���ڣ�2���������£����M���߶�BC��һ���㣬EN��EM��ֱ��BF�ڵ�N����PΪ�߶�MN���е㣬����M�ӵ�B���C�˶�ʱ����tan��ENM��ֵ��α仯����˵�����ɣ��ڵ�M�����Cʱ��ֱ��д����P������·�߳���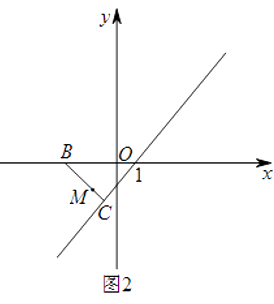
���𰸡�
��1���⣺��������C1��y=ax2+bx�� ![]() ��a��0��������A��1��0����B����3��0����
��a��0��������A��1��0����B����3��0����
�� 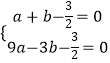 ���
��� ![]() ��
��
��������C1�Ľ���ʽΪy= ![]() x2+x��
x2+x�� ![]() ��
��
��y= ![]() x2+x��
x2+x�� ![]() =
= ![]() ��x+1��2��2��
��x+1��2��2��
�ඥ��C������Ϊ����1����2��
��2���⣺��ͼ1����CH��x����H��
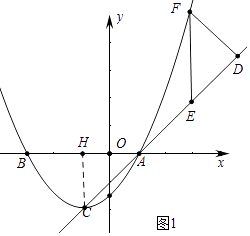
��A��1��0����C����1����2����
��AH=CH=2��
���CAB=��ACH=45�㣬
��ֱ��AC�Ľ���ʽΪy=x��1��
�ߡ�DEF����EFΪ�ĵ���ֱ�������Σ�
���DEF=45�㣬
���DEF=��ACH��
��EF��y�ᣬ
��DE=AC=2 ![]() ��
��
��EF=4��
��F��m�� ![]() m2+m��
m2+m�� ![]() ������E��m��m��1����
������E��m��m��1����
�ࣨ�� ![]() m2+m��
m2+m�� ![]() ������m��1��=4��
������m��1��=4��
���m=��3���ᣩ��m=3��
��F��3��6��
��3���⣺��tan��ENM��ֵΪ��ֵ���������仯��
��ͼ2�У���EG��AC����BF��G��
��DF��AC��BC��AC��
��DF��BC��
��DF=BC=AC��
���ı���DFBC��ƽ���ı��Σ�
�ߡ�CDF=90�㣬
���ı���DFBC�Ǿ��Σ�
��EG=BC=AC=2 ![]() ��
��
��EN��EM��
���MEN=90�㣬
�ߡ�CEG=90�㣬
���CEM=��NEG��
���ENG�ס�EMC��
�� ![]() =
= ![]() ��
��
��F��3��6����EF=4��
��E��3��2����
��C����1����2����
��EC=4 ![]() ��
��
�� ![]() =
= ![]() =2��
=2��
��tan��ENM= ![]() =2��
=2��
��tan��ENM��ֵΪ��ֵ���������仯��
����ͼ3��1�У�
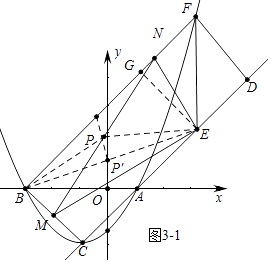
��ֱ��������EMN�У�PE= ![]() MN��ֱ��������BMN�У�PB=
MN��ֱ��������BMN�У�PB= ![]() MN��
MN��
��PE=PB��
���P��EB�Ĵ�ֱƽ�����ϣ�
���P������·�����߶�PP�䣬��ͼ3��2��
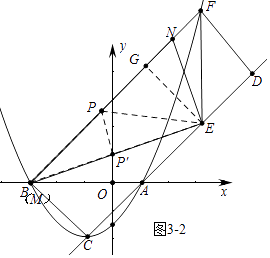
����M��B�غ�ʱ��
�ߡ�EGN�ס�ECB��
�� ![]() =
= ![]() ��
��
��EC=4 ![]() ��EG=BC=2
��EG=BC=2 ![]() ��
��
��EB=2 ![]() ��
��
�� ![]() =
= ![]() ��
��
��EN= ![]() ��
��
��PP���ǡ�BEN����λ�ߣ�
��PP��= ![]() EN=
EN= ![]() ��
��
���M�����Cʱ����P������·�߳�Ϊ ![]()
��������
��1����A��B����������뺯������ʽ�����������鼴����ý���ʽ���ٰѽ���ʽ���ɶ���ʽ������ö������ꡣ
��2����CH��x����H������A��C���������ֱ��AC�Ľ���ʽΪy=x-1�������������EF=4�����EF��y�ᣬ�����F�����꣬��ʾ����E�����꣬����EF=4���ⷽ�̼������F�����ꡣ
��3������֤���ı���DFBC�Ǿ��Σ���EG��AC����BF��G��Ȼ����ݡ�EGN�ס�EMC����Ӧ�߳ɱ������������tan��ENM��ֵ��������֤��PE=PB���ó���P��EB�Ĵ�ֱƽ�����ϣ��Ƴ���P������·�����߶�PP�䣬��ͼ3-2������M��B�غ�ʱ����֤�á�EGN�ס�ECB���������EN�ij���PP���ǡ�BEN����λ�ߣ�������λ�߶����ɵó�PP��ij���
�����㾫����ͨ�����������������λ�߶��������������ε��ж������ʣ��������������������е���߶ν��������ε���λ������������λ�߶����������ε���λ��ƽ���������εĵ����ߣ��ҵ��ڵ����ߵ�һ�룻���������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ�������Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ,����
,����![]() �ֱ��ֱ��
�ֱ��ֱ��![]() ���ڵ�
���ڵ�![]() ������
������![]() �ֱ��ֱ��
�ֱ��ֱ��![]() ���ڵ�
���ڵ�![]() ����
����![]() ������
������![]() ���˶���
���˶���![]() ����
����![]() ���㲻�غϣ�����
���㲻�غϣ�����![]() ,
,![]() ,
,![]() ��
��

��1�������![]() ��
��![]() ����֮���˶�ʱ��
����֮���˶�ʱ��![]() ֮���к�������ϵ����˵�����ɣ�
֮���к�������ϵ����˵�����ɣ�
��2�������![]() ��
��![]() ����֮���˶�ʱ��
����֮���˶�ʱ��![]() ֮���к�������ϵ����ֻ��д�����ۣ�����˵�����ɣ�
֮���к�������ϵ����ֻ��д�����ۣ�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ�����λͬѧ�ֱ���ȷָ����ijһ��������һ�����ʣ��ף�����ͼ����һ���ޣ��ң�����ͼ���������ޣ�����ÿ��һ�������ڣ�yֵ��xֵ���������С���������ǵ������������������ʽ�����ǣ� ��
A.y=2x
B.y= ![]()
C.y=�� ![]()
D.y=2x2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x-3����x2��4x+1��+4������ʽ�ֽ�Ĺ��̣�
�⣺��x2��4x=y
ԭʽ=��y-3����y+1��+4 ����һ����
= y2-2y+1 ���ڶ�����
=��y-1��2 ����������
=��x2��4x-1��2 �����IJ���
�ش��������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ��_______��
A����ȡ����ʽ�� B��ƽ���ʽ�� C.��ȫƽ����ʽ��
��2������ģ�����Ϸ������ԶԶ���ʽ��x2+2x����x2+2x+2��+1������ʽ�ֽ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AC=5��AB=3��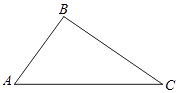
��1�����ó߹���AC���ҵ�һ��D��ʹ��DA=DC��������ͼ�ۼ�����д��������
��2������DB����DA=DC=DB�����жϡ�ABC����״��˵�����ɣ��������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�E����CDB=30�㣬CD=2 ![]() ������Ӱ���ֵ����Ϊ ��
������Ӱ���ֵ����Ϊ �� 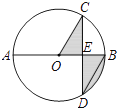
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С�������������Խ�ߣ��¶�Խ�ͣ�������С����ʾ������ı���
�������߶ȣ�ǧ�ף� | 0 | 1 | 2 | 3 | 4 | 5 |
�¶ȣ����� | 20 | 14 | 8 | 2 |
|
|
�����ϱ���������С���������漸�����⣬���С��һ��ش�
��1���ϱ���ӳ������������֮��Ĺ�ϵ���ĸ����Ա������ĸ����������
��2�������h��ʾ�������ĸ߶ȣ���t��ʾ�¶ȣ���ô����h�ı仯��t����ô�仯�ģ�
��3�����ܲ³��������6ǧ�ĸ߿��¶��Ƕ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AC��BC��BD��AD��AC ��BD ����O��AC=BD��
��֤����1��BC=AD��
��2����OAB�ǵ��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABC�У��ֱ��ӳ���AB��BC��CA��ʹ��BD��AB��CE��2BC��AF��3CA������ABC�����Ϊ1������DEF�����Ϊ( )

A. 12B. 14C. 16D. 18
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com