
【题目】如图,扇形AOD中,∠AOD=90°,OA=6,点P为![]() 上任意一点(不与点A和D重合),
上任意一点(不与点A和D重合),
PQ⊥OD于点Q,点I为△OPQ的内心,过O、I和D三点的圆的半径为r,则当点P在![]() 上运动时,求r的值.
上运动时,求r的值.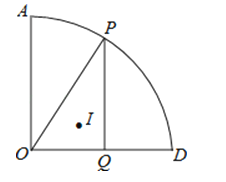
【答案】解:如图,连OI,PI,DI,
∵△OPH的内心为I,
∴∠IOP=∠IOD,∠IPO=∠IPH,
∴∠PIO=180°﹣∠IPO﹣∠IOP=180°﹣![]() (∠HOP+∠OPH),
(∠HOP+∠OPH),
而PH⊥OD,即∠PHO=90°,
∴∠PIO=180°﹣![]() (∠HOP+∠OPH)=180°﹣
(∠HOP+∠OPH)=180°﹣![]() (180°﹣90°)=135°,
(180°﹣90°)=135°,
在△OPI和△ODI中,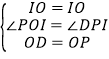 ,
,
∴△OPI≌△ODI(SAS),
∴∠DIO=∠PIO=135°,
所以点I在以OD为弦,并且所对的圆周角为135°的一段劣弧上;
过D、I、O三点作⊙O′,如图,连O′D,O′O,
在优弧DO取点P′,连P′D,P′O,
∵∠DIO=135°,
∴∠DP′O=180°﹣135°=45°,
∴∠DO′O=90°,而OD=6,
∴OO′=DO′=3![]() ,
,
∴r的值为3![]() .
.
【解析】连OI,PI,DI,由△OPH的内心为I,可得到∠PIO=180°﹣∠IPO﹣∠IOP=180°﹣![]() (∠HOP+∠OPH)=135°,并且易证△OPI≌△ODI,得到∠DIO=∠PIO=135°,所以点I在以OD为弦,并且所对的圆周角为135°的一段劣弧上;过D、I、O三点作⊙O′,如图,连O′D,O′O,在优弧AO取点P′,连P′D,P′O,可得∠DP′O=180°﹣135°=45°,得∠DO′O=90°,O′O=3
(∠HOP+∠OPH)=135°,并且易证△OPI≌△ODI,得到∠DIO=∠PIO=135°,所以点I在以OD为弦,并且所对的圆周角为135°的一段劣弧上;过D、I、O三点作⊙O′,如图,连O′D,O′O,在优弧AO取点P′,连P′D,P′O,可得∠DP′O=180°﹣135°=45°,得∠DO′O=90°,O′O=3![]() .
.
【考点精析】掌握三角形的内切圆与内心是解答本题的根本,需要知道三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.


科目:初中数学 来源: 题型:
【题目】今年9月,莉莉进入八中初一,在准备开学用品时,她决定购买若干个某款笔记本,甲、乙两家文具店都有足够数量的该款笔记本,这两家文具店该款笔记本标价都是20元/个.甲文具店的销售方案是:购买该笔记本的数量不超过5个时,原价销售;购买该笔记本超过5个时,从第6个开始按标价的八折出售:乙文具店的销售方案是:不管购买多少个该款笔记本,一律按标价的九折出售.
(1)若设莉莉要购买x(x>5)个该款笔记本,请用含x的代数式分别表示莉莉到甲文具店和乙文具店购买全部该款笔记本所需的费用;
(2)在(1)的条件下,莉莉购买多少个笔记本时,到乙文具店购买全部笔记本所需的费用与到甲文具店购买全部笔记本所需的费用相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
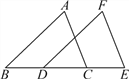
【题目】如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H.
(1)求⊙O的半径的长及线段AD的长;
(2)设PH=x,PC=y,求y关于x的函数关系式.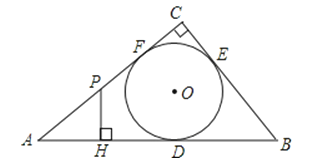
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公共汽车线路收支差额y(万元)与乘客量x(万人)的函数图象(注:收支差额=票价总收入﹣运营成本).目前这条线路亏损,为了扭亏,经市场调研,公交公司决定改革:降低运营成本,同时适当提高票价.则改革后y与x的函数图象可能是( )
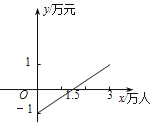
A.  B.
B. 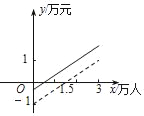
C. 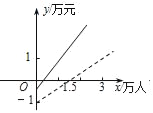 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:O是直线AB上一点,∠COD是直角,OE平分∠BOC

(1)如图1,若∠AOC=30°,求∠DOE的度数。
(2)如图1,若∠AOC=![]() ,直接写出∠DOE的度数。(用含的代数式表示)
,直接写出∠DOE的度数。(用含的代数式表示)
(3)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置,其它条件不变,探究∠AOC和∠DOE的度数之间的关系,写出结论,并说明理由。
(4)在图2中,若∠AOC内部有一条射线OF,且满足∠AOC-4∠AOF=2∠BOE,其它条件不变,试写出∠AOF与∠DOE度数的关系(不写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):如果沿直线DE折叠,则∠BDA′与∠A的关系是 .
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com