
【题目】如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )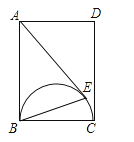
A.![]()
B.![]()
C.![]()
D.![]()
科目:初中数学 来源: 题型:
【题目】如图所示,已知锐角∠AOB及一点P.
(1)过点P作OA、OB的垂线,垂足分别是M、N;(只作图,保留作图痕迹,不写作法)
(2)猜想∠MPN与∠AOB之间的关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形AOD中,∠AOD=90°,OA=6,点P为![]() 上任意一点(不与点A和D重合),
上任意一点(不与点A和D重合),
PQ⊥OD于点Q,点I为△OPQ的内心,过O、I和D三点的圆的半径为r,则当点P在![]() 上运动时,求r的值.
上运动时,求r的值.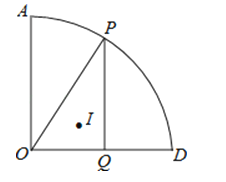
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,以AD为直径的半圆与BC相切于E,BO交半圆于F,DF的延长线交AB于点P,连DE.以下结论:①DE∥OF;②AB+CD=BC;③PB=PF;④AD2=4ABDC.其中正确的是( )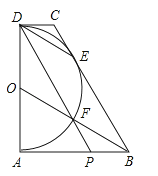
A.①②③④
B.只有①②
C.只有①②④
D.只有③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )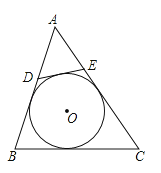
A.7
B.8
C.9
D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三种不同类型的地砖的长、宽如图所示,若现有A型地砖4块,B型地砖4块,C型地砖2块,要拼成一个正方形,则应去掉1块________型地砖;这样的地砖拼法可以得到一个关于m,n的恒等式为____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一探究活动:如图1,有甲、乙两个三角形,甲三角形内角分别为10°,20°,150°;乙三角形内角分别为80°,25°,75°.你能把每一个三角形分成两个等腰三角形吗?画一画,并标出每个等腰三角形顶角的度数.
(1)小明按要求画出了图1中甲图的分割线,请你帮他作出图1中乙图的分割线;
(2)小明进一步探究发现:能将一个顶角为108°的等腰三角形分成三个等腰三角形;请在图2中用两种不同的方法画出分割线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.如果∠A=34°,那么∠C等于( )
A.28°
B.33°
C.34°
D.56°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC,交AB于E,则下列结论一定正确的是( )
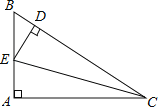
A. AE=BE B. DB=DE C. AE=BD D. ∠BCE=∠ACE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com