
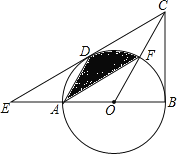
【题目】如图,在△BCE中,点A时边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)根据已知条件易证△CDO≌△CBO,即可得∠CBO=∠CDO=90°,所以CB是⊙O的切线;(2)根据条件证明△ADG≌△FOG,可得S△ADG=S△FOG,再由S阴=S扇形ODF,利用扇形面积公式计算即可.
试题解析:(1)证明:连接OD,与AF相交于点G,
∵CE与⊙O相切于点D,
∴OD⊥CE,
∴∠CDO=90°,
∵AD∥OC,
∴∠ADO=∠1,∠DAO=∠2,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠1=∠2,
在△CDO和△CBO中,
 ,
,
∴△CDO≌△CBO,
∴∠CBO=∠CDO=90°,
∴CB是⊙O的切线.

(2)由(1)可知∠3=∠BCO,∠1=∠2,
∵∠ECB=60°,
∴∠3=![]() ∠ECB=30°,
∠ECB=30°,
∴∠1=∠2=60°,
∴∠4=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴AD=OD=OF,∵∠1=∠ADO,
在△ADG和△FOG中,
 ,
,
∴△ADG≌△FOG,
∴S△ADG=S△FOG,
∵AB=6,
∴⊙O的半径r=3,
∴S阴=S扇形ODF=![]() =
=![]() .
.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
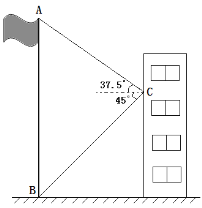
【题目】(9分)如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°.升旗时,国旗上端悬挂在距地面2.25米处. 若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?
(参考数据:sian37°=0.60,cos37°=0.80,tan37°=0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com