
【题目】如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

【答案】B.
【解析】
试题分析:(1)连接OA、OB、OP,延长BO交PA的延长线于点F.利用切线求得CA=CE,DB=DE,PA=PB再得出PA=PB=![]() r.利用Rt△BFP∽RT△OAF得出AF=
r.利用Rt△BFP∽RT△OAF得出AF=![]() FB,在RT△FBP中,利用勾股定理求出BF,再求tan∠APB的值即可.
FB,在RT△FBP中,利用勾股定理求出BF,再求tan∠APB的值即可.
试题解析:连接OA、OB、OP,延长BO交PA的延长线于点F.
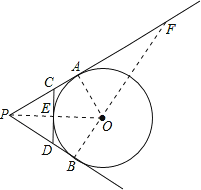
∵PA,PB切⊙O于A、B两点,CD切⊙O于点E
∴∠OAF=∠PBF=90°,CA=CE,DB=DE,PA=PB,
∵△PCD的周长=PC+CE+DE+PD=PC+AC+PD+DB=PA+PB=3r,
∴PA=PB=![]() r.
r.
在Rt△PBF和Rt△OAF中,
![]() ,
,
∴Rt△PBF∽Rt△OAF.
∴ ,
,
∴AF=![]() FB,
FB,
在Rt△FBP中,
∵PF2-PB2=FB2
∴(PA+AF)2-PB2=FB2
∴(![]() r+
r+![]() BF)2-(
BF)2-(![]() r)2=BF2,
r)2=BF2,
解得BF=![]() r,
r,
∴tan∠APB= ,
,
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了了解我区某校“校园阅读”的建设情况,检查组随机抽取40名学生,调查他们一周阅读课外书籍的时间,并将结果绘成了频数分布直方图,我们把每一个直方图的时间与学生数的积看成直方图的“面积”,时间为横轴,学生人数为纵轴构成直角坐标系,规定点M的坐标为(2,10),直线m经过点(2,0)交直方图于一点G,直线m把四个直方图面积分成相等两部分,则G点坐标为.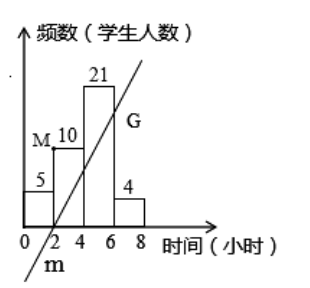
查看答案和解析>>
科目:初中数学 来源: 题型:
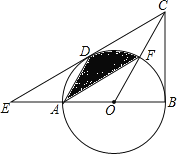
【题目】如图,在△BCE中,点A时边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1 , B1 , C1 , 使A1B=AB,B1C=BC,C1A=CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 . 第二次操作:分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使A2B1=A1B1 , B2C1=B1C1 , C2A1=C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , …按此规律,要使得到的三角形的面积超过2017,最少经过多少次操作( )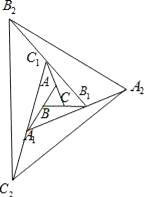
A.4
B.5
C.6
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com