
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的关系是___;
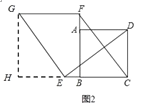
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.

【答案】(1)FG=CE,FG∥CE;(2)成立;(3)成立.
【解析】试题分析:(1)只要证明四边形CDGF是平行四边形即可得出FG=CE,FG∥CE;
(2)构造辅助线后证明△HGE≌△CED,利用对应边相等求证四边形GHBF是矩形后,利用等量代换即可求出FG=C,FG∥CE;
(3)证明△CBF≌△DCE后,即可证明四边形CEGF是平行四边形.
试题解析:解:(1)FG=CE,FG∥CE;
(2)过点G作GH⊥CB的延长线于点H.∵EG⊥DE,∴∠GEH+∠DEC=90°.∵∠GEH+∠HGE=90°,∴∠DEC=∠HE.在△HGE与△CED中,∵∠GHE=∠DCE,∠HGE=∠DEC,EG=DE,∴△HGE≌△CED(AAS),∴GH=CE,HE=CD.∵CE=BF,∴GH=BF.∵GH∥BF,∴四边形GHBF是矩形,∴GF=BH,FG∥CH,∴FG∥CE.∵四边形ABCD是正方形,∴CD=BC,∴HE=BC,∴HE+EB=BC+EB,∴BH=EC,∴FG=EC;
(3)∵四边形ABCD是正方形,∴BC=CD,∠FBC=∠ECD=90°.在△CBF与△DCE中,∵BF=CE,∠FBC=∠ECD,BC=DC,∴△CBF≌△DCE(SAS),∴∠BCF=∠CDE,CF=DE.∵EG=DE,∴CF=EG.∵DE⊥EG,∴∠DEC+∠CEG=90°.∵∠CDE+∠DEC=90°,∴∠CDE=∠CEG,∴∠BCF=∠CEG,∴CF∥EG,∴四边形CEGF平行四边形,∴FG∥CE,FG=CE.


科目:初中数学 来源: 题型:
【题目】(1)计算:(﹣1)2018﹣8÷(﹣2)3+4×(﹣![]() )3;
)3;
(2)先化简,再求值:3(a2b﹣2ab2)﹣(3a2b﹣2ab2),其中|a﹣1|+(b+![]() )2=0.
)2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张大伯从报社以每份0.4元的价格购进了![]() 份报纸,以每份0.5元的价格售出了
份报纸,以每份0.5元的价格售出了![]() 份报纸,剩余的以每份0.2元的价格退回报社,则张大伯卖报收入()元
份报纸,剩余的以每份0.2元的价格退回报社,则张大伯卖报收入()元
A. 0.7b-0.6a B. 0.5b-0.2a C. 0.7b-0.6a D. 0.3b-0.2a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数-2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数-2017将与圆周上的哪个数字重合( )
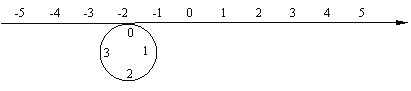
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数﹣2表示的点重合,则数轴上数﹣4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:

若数轴上数﹣3表示的点与数1表示的点重合.(根据此情境解决下列问题)
①则数轴上数3表示的点与数_______________表示的点重合.
②若点A到原点的距离是5个单位长度,并且A、B两点经折叠后重合,则B点表示的数是_________.
③若数轴上M、N两点之间的距离为2010,并且M、N两点经折叠后重合,
如果M点表示的数比N点表示的数大,则M点表示的数是________.则N点
表示的数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )

A、120° B、135° C、150° D、45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C
与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C ![]() 在抛物线上,直线AC与y轴交于点D.
在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴的正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m , 求AN的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题12分)如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别O(0,0),A(3, ![]() ),B(9,5
),B(9,5 ![]() ),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3,
),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3, ![]() ,
, ![]() (单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
(单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
(1)求AB所在直线的函数表达式.
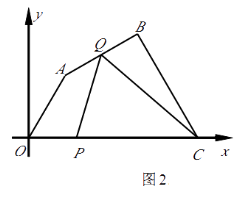
(2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值.
(3)在P,Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com