
如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.
(1)求tan∠DBC的值;
(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
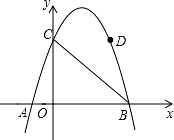
解:(1)令y=0,则﹣x2+3x+4=﹣(x+1)(x﹣4)=0,
解得 x1=﹣1,x2=4.
∴A(﹣1,0),B(4,0).
当x=3时,y=﹣32+3×3+4=4,
∴D(3,4).
如图,连接CD,过点D 作DE⊥BC于点E.
作DE⊥BC于点E.
∵C(0,4),
∴CD∥AB,
∴∠BCD=∠ABC=45°.
在直角△OBC中,∵OC=OB=4,
∴BC=4 .
.
在直角△CDE中,CD=3.
∴CE=ED=
 ,
,
∴BE=BC﹣DE=
 .
.
∴tan∠DBC= =
= ;
;
(2)过点P作PF⊥x轴于点F.
∵∠CBF=∠DBP=45°,
∴∠PBF=∠DBC,
∴tan∠PBF= .
.
设P(x,﹣x2+3x+4),则 =
= ,
,
解得 x1=﹣ ,x2=4(舍去),
,x2=4(舍去),
∴P(﹣ ,
, ).
).



 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心 ,则∠AIB的度数是( )
,则∠AIB的度数是( )
A.120° B.125° C.135° D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
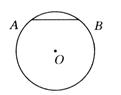
如图3-198所示,弦AB的长为6 cm,圆心O到AB的距离为4 cm,则⊙O的半径为 ( )
A.3 cm B.4 cm C.5 cm D.6 cm
cm D.6 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
如图3-205所示,已知⊙O的半径为5 cm,弦AB的长为8 cm,P是AB延长线上一点,BP=2 cm,则tan∠OPA等于 ( )
A.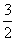 B.
B.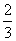 C.2 D.
C.2 D.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
(1)已知x2-4=0,求代数式x(x+1)2-x(x2+x)-x -7的值.
-7的值.
(2)先化简,再求值:(x+3)2+(x+2)(x-2)-2x2,其中x=- .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com