练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AD是ΔABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，BC恰好平分∠ABF，下列结论错误的是（ ）

    A.DE=DFB.AC=3DFC.BD=DCD.AD⊥BC

    【答案】B

    【解析】

    根据角平分线的定义和平行线的性质得出AB=AC，根据等腰三角形的性质三线合一得到BD=CD，AD⊥BC，故C、D正确；通过△CDE≌△BDF，得到DE=DF，CE=BF，故A正确．

    ∵BF∥AC，∴∠C=∠CBF．

    ∵BC平分∠ABF，∴∠ABC=∠CBF，∴∠C=∠ABC，∴AB=AC．

    ∵AD是△ABC的角平分线，∴BD=CD，AD⊥BC，故C、D正确．

    在△CDE与△BDF中，∵，∴△CDE≌△BDF，∴DE=DF，CE=BF，故A正确；

    不能得出AC=3DF，故B错误．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O为坐标原点，四边形OABC为长方形，A(10，0)，C(0，4)，D是OA的中点，点P在线段BC上运动．

    （1）B的坐标为_________；

    （2）当∠POD＝30°时，求CP的长；

    （3）当△DPO是腰长为5的等腰三角形时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在两个全等的等腰直角三角形ABC和EDC中，∠ACB＝∠ECD＝90°，点A与点E重合，点D与点B重合．现△ABC不动，把△EDC绕点C按顺时针方向旋转，旋转角为α(0°＜α＜90°)．

    (1)如图②，AB与CE交于点F，ED与AB，BC分别交于点M，H.求证：CF＝CH；

    (2)如图③，当α＝45°时，试判断四边形ACDM的形状，并说明理由；

    (3)如图②，在△EDC绕点C旋转的过程中，连结BD，当旋转角α的度数为多少时，△BDH是等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（初步探索）

    截长补短法，是初中几何题中一种添加辅助线的方法，也是把几何题化难为易的一种策略．截长就是在长边上截取一条线段与某一短边相等，补短就是通过延长或旋转等方式使两条短边拼合到一起，从而解决问题．

    （1）如图1，△ABC是等边三角形，点D是边BC下方一点，∠BDC＝120°，探索线段DA、DB、DC之间的数量关系；

    （灵活运用）

    （2）如图2，△ABC为等边三角形，直线a∥AB，D为BC边上一点，∠ADE交直线a于点E，且∠ADE＝60°．求证：CD＋CE＝CA；

    （延伸拓展）

    （3）如图3，在四边形ABCD中，∠ABC＋∠ADC＝180°，AB＝AD．若点E在CB的延长线上，点F在CD的延长线上，满足EF＝BE＋FD，请直接写出∠EAF与∠DAB的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ACB中，AC=BC=8，O为AB的中点，以O为直角顶点作等腰直角三角形OEF,与边AC，BC相交于点M，N.有下列结论：①AM=CN；②CM+CN=8；③；④当M是AC的中点时，OM=ON.其中正确结论的序号是______.

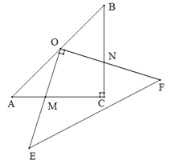
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC≌△A′B′C，∠ACB=90°，∠B=50°，点B′在线段AB上，AC，A′B′交于点O，则∠COA′的度数是（ ）

    A.50°B.60°

    C.45°D.80°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）课本习题回放：如图①,∠ACB=90°,AC=BC, AD⊥CE,BE⊥CE,垂足分别为D,E，AD=2.5cm，DE=1.7cm..求BE的长.

    （2）探索证明：如图②，点B、C在∠MAN的边AM、AN上，点E, F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC,∠1=∠2=∠BAC.求证：△ABE≌△CAF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，连接BD，点O是BD的中点，若M、N是边AD上的两点，连接MO、NO，并分别延长交边BC于两点M′、N′，则图中的全等三角形共有（　　）

    A. 2对 B. 3对 C. 4对 D. 5对

    查看答案和解析>>

    同步练习册答案