Question

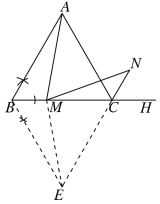
【题目】如图，在等边中，是边上一点（不含端点 ，），是的外角 的平分线上一点，且．

（1）尺规作图：在直线的下方，过点作，作的延长线，与相交于点.

（2）求证：是等边

（3）求证：.

Answer 1

【答案】（1）见解析；（2）见解析；（3）见解析

【解析】

（1）根据尺规作图，作一个角等于已知角的做法作出∠CBE，再延长NC与BE交于E；

（2）由△ABC是等边三角形，易得∠CBE=∠BCE=60°，从而判定等边三角形；

（3）连接EM，易证△ABM≌△EBM，推出ME=MN，得到∠MEN=∠MNE，再利用∠NMC+∠MNE=∠BEM+∠MEN=60°，推出∠NMC=∠BEM=∠BAM，最后由等量代换可得出∠AMB+∠NMC=120°，从而得到∠AMN=60°.

（1）如图所示，

（2）证明：∵△ABC为等边三角形

∴∠CBA=∠ACB=60°，

∴∠ACH=180°-60°=120°，

又∵CN平分∠ACH

∴∠NCH=∠ACH=60°

∴∠BCE=∠NCH=60°

又∵∠CBE=∠CBA

∴在△BEC中，

∠CBE=∠BCE=∠BEC=60°，

∴△BEC是等边△BEC.

（3）连接EM，

∵△ABC和△BEC都是等边三角形，

∴AB=BC=BE，∠ABM=∠EBM=60°，

在△ABM和△EBM中，

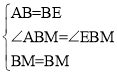
∴△ABM≌△EBM（SAS）

∴AM=EM，∠BAM=∠BEM，

又∵AM=MN

∴EM=MN，

∴∠MEN=∠MNE

∵∠NCH=∠NMC+∠MNE=60°，∠BEM+∠MEN=60°

∴∠NMC=∠BEM

∴∠NMC=∠BEM=∠BAM

∵∠BAM+∠AMB=180°-∠ABM=120°

∴∠AMB+∠NMC=120°

∴∠AMN=180°-（∠AMB+∠NMC）=60°.