
����Ŀ��ij��ҵΪ��������г���������![]() ��
��![]() ���ֲ�Ʒ��ֻѡ��һ�ֽ���Ͷ����������֪Ͷ�����������ֲ�Ʒ���й��������±�������λ������Ԫ��
���ֲ�Ʒ��ֻѡ��һ�ֽ���Ͷ����������֪Ͷ�����������ֲ�Ʒ���й��������±�������λ������Ԫ��
��Ŀ ���� | ��̶� �ɱ� | ÿ����Ʒ �ɱ� | ÿ����Ʒ ���ۼ� | ÿ������ �����ļ��� |
|
|
|
|
|
|
|
|
|
|
������̶��ɱ����������ļ����أ�![]() Ϊ������������ֵ������
Ϊ������������ֵ������![]() ��Ʒ��ԭ���ϼ۸������Ԥ��
��Ʒ��ԭ���ϼ۸������Ԥ��![]() �����⣬������
�����⣬������![]() ��
��![]() ��Ʒʱ���Ͻ�
��Ʒʱ���Ͻ�![]() ����Ԫ���ر��˰���������������IJ�Ʒ�����ڵ������۳�ȥ��
����Ԫ���ر��˰���������������IJ�Ʒ�����ڵ������۳�ȥ��
![]() д���ó��ֱ�Ͷ������
д���ó��ֱ�Ͷ������![]() ��
��![]() ���ֲ�Ʒ��������
���ֲ�Ʒ��������![]() ��
��![]() ��������Ӧ��Ʒ�ļ���
��������Ӧ��Ʒ�ļ���![]() ֮��ĺ�����ϵ��ָ�����Ա���ȡֵ��Χ��
֮��ĺ�����ϵ��ָ�����Ա���ȡֵ��Χ��
![]() ���Ͷ�ʲſɻ��������������������滮��
���Ͷ�ʲſɻ��������������������滮��
���𰸡�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ʱ��Ͷ������
ʱ��Ͷ������![]() ��Ʒ
��Ʒ![]() ���ɻ�����������
���ɻ�����������![]() ʱ������
ʱ������![]() ��Ʒ������
��Ʒ������![]() ��Ʒ���ɻ�����������
��Ʒ���ɻ�����������![]() ʱ��Ͷ������
ʱ��Ͷ������![]() ��Ʒ
��Ʒ![]() ���ɻ�����������
���ɻ�����������
��������
��1������=����������-�̶��ɱ�-��Ʒ�ɱ�-�ر��˰������øó��ֱ�Ͷ������A��B���ֲ�Ʒ��������y1��y2��������Ӧ��Ʒ�ļ���x֮��ĺ�����ϵ���Ա���ȡֵ��Χ��
��2������Ƚ�������y1��y2�Ĵ�С����ȷ������ط�����
![]() ����������Ϊ
����������Ϊ![]() ����������ļ��㹫ʽ��������
����������ļ��㹫ʽ��������![]() ��
��![]() ����Ʒ��������
����Ʒ��������![]() ��
��![]() �ֱ�Ϊ��
�ֱ�Ϊ��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
��2����![]() ����
����![]() ����
����![]() ����������
����������
�֡�![]() ��
��
�൱![]() ʱ������
ʱ������![]() ��Ʒ���������Ϊ
��Ʒ���������Ϊ![]() ������Ԫ����
������Ԫ����
�֡�![]() ��
��![]() ��
��
�൱![]() ʱ������
ʱ������![]() ��Ʒ���������Ϊ
��Ʒ���������Ϊ![]() ������Ԫ����
������Ԫ����
���������о��������ֲ�Ʒ���������Ϊ�ˣ���������Ƚϣ�
������![]() ��Ʒ�������Ϊ
��Ʒ�������Ϊ![]() ������Ԫ��������
������Ԫ��������![]() ��Ʒ�������Ϊ
��Ʒ�������Ϊ![]() ������Ԫ����
������Ԫ����
��![]() ����
����![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
���ԣ���![]() ʱ��Ͷ������
ʱ��Ͷ������![]() ��Ʒ
��Ʒ![]() ���ɻ�����������
���ɻ�����������
��![]() ʱ������
ʱ������![]() ��Ʒ������
��Ʒ������![]() ��Ʒ���ɻ�����������
��Ʒ���ɻ�����������
��![]() ʱ��Ͷ������
ʱ��Ͷ������![]() ��Ʒ
��Ʒ![]() ���ɻ�����������
���ɻ�����������


 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������A��ʾС���ң���B��ʾѧУ��С�������ﳵ����С��ȥѧУ������C��ʱ������ѧ��û�����������������ﳵԭ·�ؼ����������С����ͬʱС������ȥѧУ������ѧУ��ȴ���������������ʱ����Բ��ƣ�С���������������˶������зֱ𱣳������������C������x����ʱ��C���ľ���Ϊy1����С����C���ľ���Ϊy2������ͼ�ڣ�����O-D-E-F��ʾy1��x�ĺ���ͼ��������O-G-F��ʾy2��x�ĺ���ͼ����

��1��С�����ٶ�Ϊ_________m/min��ͼ����a��ֵΪ__________��
��2���������C������x����ʱ������С��֮��ľ���Ϊy����
��д��С���������ﳵ��C�����ص�A���Ĺ����У�y��x�ĺ�������ʽ��x��ȡֵ��Χ��

����ͼ���л�������������y��x�ĺ���ͼ������Ҫ�����ؼ����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
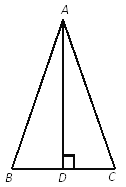
����Ŀ����ͼ����ABC�У�AD��BC��������D��С��˵����AB��BD��AC��CDʱ������ABC�ǵ��������Σ�����˵����ȷ������ȷ����֤�����粻��ȷ����ٷ���˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������4��ȫ�ȵ�С��������1��С���������̶��ɵ�������ͼ��.��֪��ͼ�������Ϊ49��С�����ε����Ϊ4�����ֱ���x��y(x >y)��ʾС�����εij��Ϳ��������й�ϵʽ�в���ȷ����( )

A. x+y=7 B. x-y=2 C. x2 +y2=25 D. 4xy+4=49
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
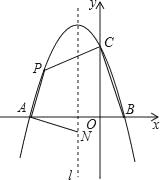
����Ŀ����ͼ��������y=ax2+bx+c��x�ύ�ڵ�A�͵�B��1��0������y�ύ�ڵ�C��0��3������Գ���lΪx=��1��
��1���������ߵĽ���ʽ��д���䶥�����ꣻ
��2��������P�ڵڶ������ڵ��������ϣ�����N�ڶԳ���l�ϣ�
����PA��NA����PA=NAʱ�����ʱ��P�����ꣻ
�����ı���PABC��������ʱ�����ı���PABC��������ֵ����ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�![]() �У�
��![]() ��
��![]() ����һ�㣨�����˵�
����һ�㣨�����˵� ![]() ��
��![]() ����
����![]() ��
��![]() �����
����� ![]() ��ƽ������һ�㣬��
��ƽ������һ�㣬��![]() ��
��

��1���߹���ͼ����ֱ��![]() ���·�������
���·�������![]() ��
��![]() ����
����![]() ���ӳ��ߣ���
���ӳ��ߣ���![]() �ཻ�ڵ�
�ཻ�ڵ�![]() .
.
��2����֤��![]() �ǵȱ�
�ǵȱ�![]()
��3����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
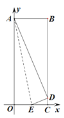
����Ŀ����ͼ���ֱ��Գ�����OABC�ı�OC��OA����ֱ��Ϊx�ᡢy�ᣬ����ƽ��ֱ���� ��ϵ.��֪AO=13��AB=5����E���߶�OC�ϣ���ֱ��AEΪ�ᣬ����OAE���ۣ���O�Ķ�Ӧ��Dǡ�������߶�BC��.���E������Ϊ_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺����һ����λ������N�ĸ�λ������ʮλ����֮����������6�����һ���µ���λ�������dz������λ��ΪN����������������34����������Ϊ364��������һ����λ������M��6��õ�һ�����������dz��������ΪM����������������34����������Ϊ40����
��1��30���������������� ������������������ ����
��2����֤��������һ����λ������A��������������������������֮���ܱ�9������
��3����һ����λ������B���������ĸ�λ����֮����B����������λ����֮�͵�һ�룬��B�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ڵȱ���ABC�У���D.E�ֱ��ڱ�BC��AB�ϣ���BD=AE��AD��CE���ڵ�F��
��1����֤��AD=CE
��2�����DFC�Ķ���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com