
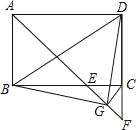
【题目】如图,在ABCD中,AD>AB,AM、BN、CP、DQ为四个内角的角平分线,P、为AD边上两点,其中AM与DQ相交于E,BN与CP相交于F,AM与BN相交于G,CP与DQ相交于H.
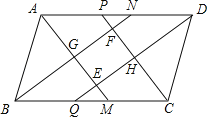
(1)求证:四边形EHFG是矩形.
(2)ABCD满足 时,四边形EHFG为正方形;ABCD满足 时,F点落在AD边上.(与点P、点N重合)
(3)探究矩形EHFG的对角线长度与ABCD的边长之间的数量关系,并证明.
【答案】(1)见解析; (2)∠BAD=90°,且BC=2AB ;BC=2AB;(3)GH=BC﹣AB;证明见解析.
【解析】
(1)根据平行线的性质及角平分线的定义证明四边形EHFG有三个角是直角即可;
(2)由(1)可得,四边形EHFG是矩形,若四边形EHFG为正方形,则有一组临边相等即可;若F点落在AD边上.(与点P、点N重合),则可得由(1)得:AF=AB,DF=CD,AG⊥BN,利用平行四边形的性质等量代换即可得到AB与BC的关系.
(3)连接EF、GH,由(1)(2)结论证四边形BQDN是平行四边形,四边形GHQB是平行四边形,即可得到其数量关系.
(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠ABC=180°.
∵AM,BN分别平分∠DAB,∠ABC,
∴∠MAB+∠NBA=![]() (∠DAB+∠ABC)=×180°=90°.
(∠DAB+∠ABC)=×180°=90°.
∴∠EGF=∠AGB=90°,
同理:∠EHF=90°,∠GEH=90°,
∴四边形EHFG是矩形;
(2)ABCD满足∠BAD=90°,且BC=2AB时,四边形EHFG为正方形;理由如下:
此时F点落在AD边上,与点P、点N重合,如图1所示:
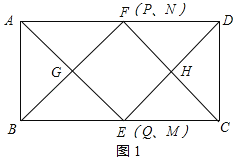
由(1)得:四边形EHFG是矩形,AG⊥BN,
∵AD∥BC,
∴∠AFB=∠CBF,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠AFB=∠ABF,
∴AF=AB,
同理:DF=CD,
∴AF=AB=BE,
∵∠BAD=90°,
∴△BAF、△ABE是等腰直角三角形,
∵AE⊥BF,
∴BG=FG,AG=EG,
∴AG=![]() BF=BG=FG,
BF=BG=FG,
∴FG=EG,
∴四边形EHFG为正方形,
故答案为:∠BAD=90°,且BC=2AB;
ABCD满足BC=2AB时,F点落在AD边上.(与点P、点N重合);理由如下:
如图2所示:
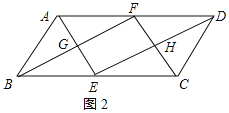
由(1)得:AF=AB,DF=CD,AG⊥BN,
∴AF=DF=AB,
∴AD=2AB,
∴BC=2AB,
故答案为:BC=2AB;
(3)矩形EHFG的对角线长度与ABCD的边长之间的数量关系为GH=BC﹣AB;理由如下:如图3所示:连接EF、GH
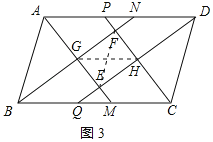
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∵四边形EHFG是矩形,
∴GH=EF,BN∥DQ,
∴四边形BQDN是平行四边形,
∴BN=DQ,
同(1)(2)得:AG⊥BN,AN=AB,CQ=CD=AB,
∴BG=NG,
同理:
∴BG=QH,
∴四边形GHQB是平行四边形,
∴GH=BQ=BC﹣CQ=BC﹣AB.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
①BE=CD;
②∠DGF=135°;
③△BEG≌△DCG;
④∠ABG+∠ADG=180°;
⑤若![]() ,则3S△BDG=13S△DGF.
,则3S△BDG=13S△DGF.
其中正确的结论是_____.(请填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用960元购进一批服装,并以每件46元的价格全部售完![]() 由于服装畅销,服装店又用2220元,再次以比第一次进价多5元的价格购进服装,数量是第一次购进服装的2倍,仍以每件46元的价格出售.
由于服装畅销,服装店又用2220元,再次以比第一次进价多5元的价格购进服装,数量是第一次购进服装的2倍,仍以每件46元的价格出售.
![]() 该服装店第一次购买了此种服装多少件?
该服装店第一次购买了此种服装多少件?
![]() 两次出售服装共盈利多少元?
两次出售服装共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
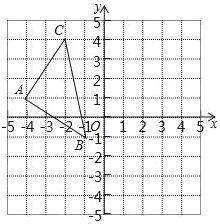
【题目】已知,△ABC在平面直角坐标系中的位置如图所示.
(1)把△ABC向下平移2个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)请画出△A1B1C1关于y轴对称的△A2B2C2,并写出A2的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点 A,B的坐标分别为(0,3),(1,0),△ABC是等腰直角三角形,∠ABC=90°.
(1)图1中,点C的坐标为 ;
(2)如图2,点D的坐标为(0,1),点E在射线CD上,过点B 作BF⊥BE交y轴于点F.
①当点E为线段CD的中点时,求点F的坐标;
②当点E在第二象限时,请直接写出F点纵坐标y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过12吨(含12吨)时,每吨按政府补贴优惠价收费;每月超过12吨,超过部分每吨按市场调节价收费,小黄家1月份用水24吨,交水费42元.2月份用水20吨,交水费32元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少元;
(2)设每月用水量为![]() 吨,应交水费为
吨,应交水费为![]() 元,写出
元,写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)小黄家3月份用水26吨,他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
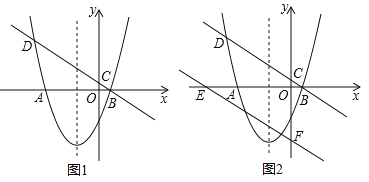
【题目】如图1,抛物线y=ax2+2x+c与x轴交于A(﹣4,0),B(1,0)两点,过点B的直线y=kx+![]() 分别与y轴及抛物线交于点C,D.
分别与y轴及抛物线交于点C,D.
(1)求直线和抛物线的表达式;
(2)动点P从点O出发,在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒,当t为何值时,△PDC为直角三角形?请直接写出所有满足条件的t的值;
(3)如图2,将直线BD沿y轴向下平移4个单位后,与x轴,y轴分别交于E,F两点,在抛物线的对称轴上是否存在点M,在直线EF上是否存在点N,使DM+MN的值最小?若存在,求出其最小值及点M,N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】奉节脐橙是重庆市奉节县特产,中国地理标志产品,眼下,正值奉节脐橙销售旺季,某商家看准商机,第一次用4800元购进一批奉节脐橙,销售良好,于是第二次又用12000元购进一批奉节脐橙,但此时进价比第一次涨了2元,所购进的数量恰好是第一次购进数量的两倍.
(1)求第一次购进奉节脐橙的进价.
(2)实际销售中,两次售价均相同,在销售过程中,由于消费者挑选后,果品下降,第一批奉节脐橙的最后100千克八折售出,第二批奉节脐橙的最后800千克九折售出,若售完这两批奉节脐橙的获利不低于9400元,则售价至少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com