
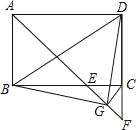
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
①BE=CD;
②∠DGF=135°;
③△BEG≌△DCG;
④∠ABG+∠ADG=180°;
⑤若![]() ,则3S△BDG=13S△DGF.
,则3S△BDG=13S△DGF.
其中正确的结论是_____.(请填写所有正确结论的序号)
【答案】①③④⑤
【解析】
①根据矩形的性质可得出∠BAD=∠ABC=90°,AB=CD,再由角平分线的性质可得出∠BAE=45°,通过角的计算即可得出∠BAE=∠BEA,从而得出AB=BE=CD,即①正确;②根据平行线的性质以及对顶角相等可得出△CEF为等腰直角三角形,由此得出∠CGF=90°,∠FCG=45°,根据三角形外角的性质可得出∠CGD<45°,再由角的关系即可得出∠DGF=∠CGD+∠CGF<135°,即②不正确;③通过角的计算可得出∠BEG=∠DCG,再根据等腰直角三角形的性质可得出CG=EG,由此即可利用全等三角形的判定定理(SAS)证出△BEG≌△DCG,即③正确;④由③可得出∠EBG=∠CDG,根据角的计算即可得出∠ABG+∠ADG=180°,即④正确;⑤过点G作GM⊥DF于点M,设AB=2a(a>0),则AD=3a,利用分割图形求面积法结合三角形的面积公式可算出S△BDG和S△DGF的值,由此可得出⑤正确.综上即可得出结论.
解:①∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,AB=CD,
∵AE是∠BAD的角平分线,
∴∠BAE=∠DAE=45°,
∴∠AEB=90°﹣∠BAE=45°=∠BAE,
∴BE=AB=CD,①正确;
②∵AB∥CD,
∴∠CFE=∠BAE=45°,∠CEF=∠AEB=45°,
∴△CEF为等腰直角三角形,
∵点G为EF的中点,
∴CG⊥EF,∠CGF=90°,∠FCG=45°,
∵∠FCG=∠CGD+∠CDG=45°,
∴∠CGD<45°,
∴∠DGF=∠CGD+∠CGF<45°+90°=135°,②不正确;
③∵△CEF为等腰直角三角形,
∴CG=EG.
∵∠BEG=180°﹣∠CEF=135°,∠DCG=180°﹣∠FCG=135°,
∴∠BEG=∠DCG,
在△BEG和△DCG中,有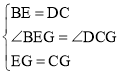 ,
,
∴△BEG≌△DCG(SAS),③正确;
④∵△BEG≌△DCG,
∴∠EBG=∠CDG,
∵∠ABG=∠ABC+∠EBG,∠ADG=∠ADC﹣∠CDG,
∴∠ABG+∠ADG=∠ABC+∠ADC=180°,④正确;
⑤过点G作GM⊥DF于点M,如图所示.
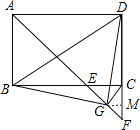
∵![]() =
=![]() ,
,
∴设AB=2a(a>0),则AD=3a.
∵∠DAF=45°,∠ADF=90°,
∴△ADF为等腰直角三角形,
∴DF=AD=3a.
∵△CGF为等腰直角三角形,
∴GM=CM=![]() CF=
CF=![]() (DF﹣CD)=
(DF﹣CD)=![]() a,
a,
∴S△DGF=![]() DFGM=
DFGM=![]() ×3a×
×3a×![]() a=
a=![]() .
.
S△BDG=S△BCD+S梯形BGMC﹣S△DGM=![]() ×2a×3a+
×2a×3a+![]() ×(3a+
×(3a+![]() a)×
a)×![]() a﹣
a﹣![]() ×
×![]() a×(2a+
a×(2a+![]() a)=
a)=![]() .
.
∴3S△BDG=13S△DGF,⑤正确.
综上可知:正确的结论有①③④⑤.
故答案为:①③④⑤.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,过点D向AB,AC两边作垂线,垂足分别为E,F,那么下列结论中不一定正确的是( )

A. BD=CD B. DE=DF C. AE=AF D. ∠ADE=∠ADF
查看答案和解析>>
科目:初中数学 来源: 题型:
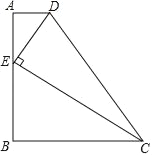
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.
(1)求证:△ADE∽△BEC.
(2)若AD=1,BC=3,AE=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量建筑物AB的高度,在D处树立标杆CD,标杆的高是2m,在DB上选取观测点E、F,从E测得标杆和建筑物的顶部C、A的仰角分别为58°、45°.从F测得C、A的仰角分别为22°、70°.求建筑物AB的高度(精确到0.1m).(参考数据:tan22°≈0.40,tan58°≈1.60,tan70°≈2.75.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )
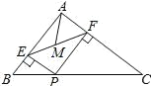
A.1B.1.3C.1.2D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
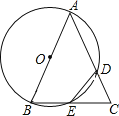
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
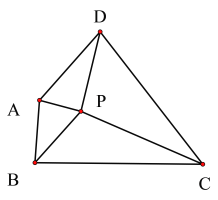
【题目】如图,四边形ABCD中,∠A、∠B 、∠C、 ∠D 的角平分线恰相交于一点P,记作△APD、△APB、△BPC、△DPC的面积分别为![]() 、
、![]() 、
、![]() 、
、![]() 则下列关系式正确的是( )
则下列关系式正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
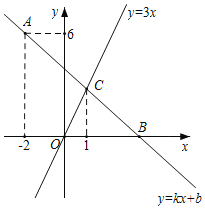
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,6),且与x轴相交于点B,与正比例函数y=3x的图象交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴上,且满足S△COD=S△BOC,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AD>AB,AM、BN、CP、DQ为四个内角的角平分线,P、为AD边上两点,其中AM与DQ相交于E,BN与CP相交于F,AM与BN相交于G,CP与DQ相交于H.
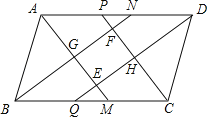
(1)求证:四边形EHFG是矩形.
(2)ABCD满足 时,四边形EHFG为正方形;ABCD满足 时,F点落在AD边上.(与点P、点N重合)
(3)探究矩形EHFG的对角线长度与ABCD的边长之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com