
【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )
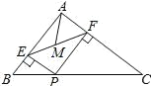
A.1B.1.3C.1.2D.1.5
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
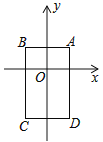
A. (﹣1,﹣2) B. (―1,1)
C. (-1,-1) D. (1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
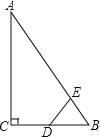
A.2B.2.5或3.5
C.3.5或4.5D.2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
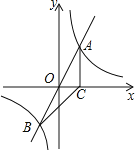
【题目】如图, 正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
(1)求k的值
(2)x轴上是否存在一点D,使ΔABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并填写理由:如图,AD∥BE,∠1=∠2,那么∠A与∠E相等吗?请完成解答过程:
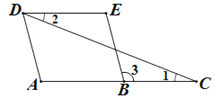
解:∵AD∥BE(已知)
∠A=∠_____ (_________________)
又∵∠1=∠2 (______)
∴AC∥_____ (________________)
∴∠3=∠_____(两直线平行,内错角相等)
∴∠A=∠______ (_______)
查看答案和解析>>
科目:初中数学 来源: 题型:
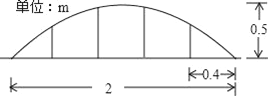
【题目】某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管(如图)做成立柱,为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.
(1)求此抛物线的解析式;
(2)计算所需不锈钢管的总长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系第一象限中,已知点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度匀速向点
个单位长度的速度匀速向点![]() 方向运动,与此同时,
方向运动,与此同时,![]() 轴上动点
轴上动点![]() 从点
从点![]() 出发,以相同的速度向右运动, 两动点运动时间为:
出发,以相同的速度向右运动, 两动点运动时间为:![]() , 以
, 以![]() 分别为边作矩形
分别为边作矩形![]() , 过点
, 过点![]() 作双曲线交线段
作双曲线交线段![]() 于点
于点![]() ,作
,作![]() 中点
中点![]() ,连接
,连接![]()
(1)当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(2)若![]() 平分
平分![]() , 则
, 则![]() 的值为多少?
的值为多少?
(3)若![]() 为直角, 则
为直角, 则![]() 的值为多少?
的值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com