
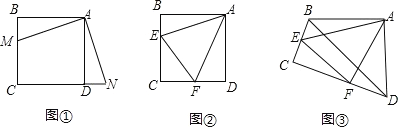
【题目】(1)如图①,点 M 是正方形 ABCD 的边 BC 上一点,点 N 是 CD 延长线上一点, 且BM=DN,则线段 AM 与 AN 的关系.
(2)如图②,在正方形 ABCD 中,点 E、F分别在边 BC、CD上,且∠EAF=45°,判断 BE,DF,EF 三条线段的数量关系,并说明理由.
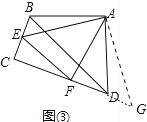
(3)如图③,在四边形 ABCD中,AB=AD,∠BAD=90°,∠ABC+∠ADC=180°,点E、F分别在边 BC、CD 上,且∠EAF=45°,若 BD=5,EF=3,求四边形 BEFD 的周长.
【答案】(1)结论:AM=AN,AM⊥AN.理由见解析;(2)BE+DF=EF;(3)四边形BEFD的周长为11.
【解析】
(1)利用正方形条件证明△ABM≌△ADN,即可推出结论,
(2)过点 A 作 AG⊥AE 交 CD 延长线于点 G,证明△ABE≌△ADG得AE=AG,∠EAF=∠GAF进而证明△AEF≌△AGF,得EF=FG即可解题,
(3)过点 A 作 AG⊥AE 交 CD 延长线于点 G.证明△ABE≌△ADG得AE=AG,∠EAF=∠GAF进而证明△AEF≌△AGF,得EF=FG即可解题.
(1)结论:AM=AN,AM⊥AN.
理由:∵四边形 ABCD 是正方形,
∴AB=AD,∠B=∠ADN=∠BAD=90°,
∵BM=DN,
∴△ABM≌△ADN,
∴AM=AN,∠BAM=∠DAN,
∴∠AMN=∠BAD=90°,
∴AM⊥AN,
(2)如图②中,过点 A 作 AG⊥AE 交 CD 延长线于点 G.

∵四边形 ABCD 为正方形,
∴AB=AD,∠B=∠BAD=∠ADC=90°.
∴∠B=∠ADG=90°,∠BAE+∠EAD=90°.
∵AG⊥AE,∴∠DAG+∠EAD=90°.
∴∠BAE=∠DAG.
在△ABE 和△ADG 中,
![]() ,
,
∴△ABE≌△ADG.
∴AE=AG,BE=DG.
∵∠EAF=45°,AG⊥AE,
∴∠EAF=∠GAF=45°.
在△FAE 和△FAG 中,
![]() ,
,
∴△AEF≌△AGF.
∴EF=FG.
∵FG=DF+DG=DF+BE,
∴BE+DF=EF.
(3)如图③中,过点 A 作 AG⊥AE 交 CD 延长线于点 G.
∵AB=AD,∠ABC+∠ADC=180°,∠ADG+∠ADC=180°
∴∠ABE=∠ADG,
∵AG⊥AE,∴∠DAG+∠EAD=90°.
∵∠BAE+∠EAD=90°
∴∠BAE=∠DAG.
在△ABE 和△ADG 中,
![]() ,
,
∴△ABE≌△ADG.
∴AE=AG,BE=DG.
∵∠EAF=45°,AG⊥AE,
∴∠EAF=∠GAF=45°.
在△FAE 和△FAG 中,
![]() ,
,
∴△AEF≌△AGF.
∴EF=FG.
∵FG=DF+DG=DF+BE,
∴BE+DF=EF.
∴四边形BEFD的周长为EF+(BE+DF)+DB=3+3+5=11.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】某电信公司推出一款移动话费套餐,资费标准见下表:
套餐月费/元 | 套餐内容 | 套餐外资费 | |
主叫限定时间/分钟 | 被叫 | 主叫超时费 (元/分钟) | |
58 | 50 | 免费 | 0.25 |
88 | 150 | 0.20 | |
118 | 350 | 0.15 | |
说明:①主叫:主动打电话给别人;被叫:接听别人打进来的电话. ②若办理的是月使用费为 58 元的套餐,主叫时间不超过 50 分钟时,当月话费即 为 58 元;主叫时间为 60 分钟,则当月话费为 58+0.25×(60-50)=60.5 元. | |||
小文办理的是月使用费为 88 元的套餐,亮亮办理的是月使用费为 118 元的套餐.
(1)小文当月的主叫时间为 220 分钟,则该月她的话费需多少元?
(2)某月小文和亮亮的主叫时间都为 m 分钟 (m 350) ,请用含 m 的代数式表示该月他们的 话费差.
(3)某月小文和亮亮的话费相同,但主叫时间比亮亮少 100 分钟,求小文和亮亮的主叫时间 分别为多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
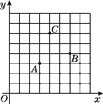
【题目】如图,A,B,C为一个平行四边形的三个顶点,且A,B,C三点的坐标分别为(3,3),(6,4),(4,6).
(1)请直接写出这个平行四边形第四个顶点的坐标;
(2)求这个平行四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数 y=2x 与 y=ax+5 的图象相交于点 A(m,4).
(1)求 A 点坐标及一次函数 y=ax+5 的解析式;
(2)设直线 y=ax+5 与 x 轴交于点 B,求△AOB 的面积;
(3)求不等式 2x<ax+5 的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)在(1)条件下,连结BD,当∠A=32°时,求∠CBD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
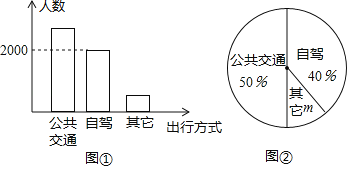
A. 本次抽样调查的样本容量是5000
B. 扇形图中的m为10%
C. 样本中选择公共交通出行的有2500人
D. 若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建立模型:
如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
操作:
过点A作AD⊥l于点D,过点B作BE⊥l于点E.求证:△CAD≌△BCE.
模型应用:
(1)如图2,在直角坐标系中,直线l1:y=![]() x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com