练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．计算：
    （1）（-1）2016+（$\frac{1}{2}$）-2-（3.14-π）0
    （2）（2x3y）2•（-2xy）-（-2x3y）3÷（2x2）

    分析 （1）直接利用负整数指数幂的性质结合零指数幂的性质化简求出答案；
    （2）直接利用积的乘方运算法则化简，进而结合单项式乘以单项式以及单项式除以单项式运算法则求出答案．

    解答 解：（1）（-1）2016+（$\frac{1}{2}$）-2-（3.14-π）0
    =1+4-1
    =4；

    （2）（2x3y）2•（-2xy）-（-2x3y）3÷（2x2）
    =4x6y2•（-2xy）+8x9y3÷（2x2）
    =-8x7y3+4x7y3
    =-4x7y3．

    点评 此题主要考查了实数运算以及整式的混合运算，正确掌握运算法则是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

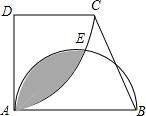    16．如图，∠D=∠DAB=90°，AD=CD=$\sqrt{3}$，AB=2，以D为圆心，AD为半径作扇形AEC，以AB为直径作半圆，则圆中阴影部分的面积为$\frac{5π}{6}-\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷（解析版） 题型：判断题

    正方形网格中（网格中的每个小正方形边长是1），△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：

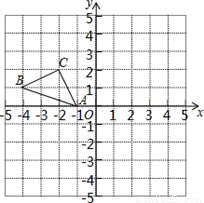
    （1）作出△ABC绕点A逆时针旋转90°的△A1B1C1；作出△ABC关于原点O成中心对称的△AB2C2；

    （2）点B1的坐标为_________，

    点C2的坐标为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，正八边形ABCDEFGH内接于圆，点P是弧GH上的任意一点，则∠CPE的度数为（　　）
    A．30°B．15°C．60°D．45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

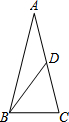    18．如图，在△ABC中，AB=AC=4，cosC=$\frac{1}{4}$，BD是中线，将△CBD沿直线BD翻折后，点C落在点E，那么AE的长为$\sqrt{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．若方程组$\left\{\begin{array}{l}{2x+y=k}\\{2x-y=1}\end{array}\right.$的解中，x是正数，y是非正数．
    （1）求k的正整数解；
    （2）在（1）的条件下求一次函数y=$kx-\frac{3}{2}$与坐标轴围成的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．已知二次函数y=ax2，其图象在对称轴左边部分，y值x的增大而增大，那么这个二次函数的解析式可以是y=-2x2（答案不唯一）（只需写一个）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

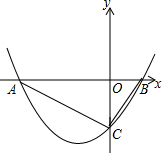    12．如图，已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A（-4，0），B（1，0）两点，与y轴交于C点，则△ABC的面积是5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

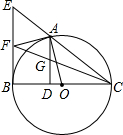    13．如图，A是以BC为直径的⊙O上的一点，AD⊥BC于点D，过点B作⊙O的切线，与CA的延长线相交于点E，点F是EB的中点，连结CF交AD于点G
    （1）求证：AF是⊙O的切线；
    （2）求证：AG=GD；
    （3）若FB=FG，且⊙O的半径长为3$\sqrt{2}$，求BD．

    查看答案和解析>>

    同步练习册答案