
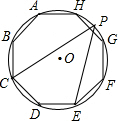
 如图,正八边形ABCDEFGH内接于圆,点P是弧GH上的任意一点,则∠CPE的度数为( )
如图,正八边形ABCDEFGH内接于圆,点P是弧GH上的任意一点,则∠CPE的度数为( )| A. | 30° | B. | 15° | C. | 60° | D. | 45° |
科目:初中数学 来源: 题型:解答题
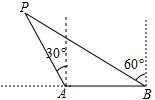 如图,海上有一小岛P,在他周围7海里内有暗礁,一艘轮船以15海里/时的速度由东向西方向航行至B点处测得小岛P在它北偏西60°的方向上,继续向西航行40分钟到达A处,又测得小岛P在它的北偏西30°方向上,如果货轮不改变方向能否继续航行?
如图,海上有一小岛P,在他周围7海里内有暗礁,一艘轮船以15海里/时的速度由东向西方向航行至B点处测得小岛P在它北偏西60°的方向上,继续向西航行40分钟到达A处,又测得小岛P在它的北偏西30°方向上,如果货轮不改变方向能否继续航行?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 测试 类别 | 平时成绩 | 期中 | 期末 | ||||
| 测试1 | 测试2 | 测试3 | 测试4 | 测试5 | |||
| 甲 | m | 99 | 100 | 99 | 98 | 96 | 95 |
| 乙 | 90 | 93 | 94 | n | 95 | 92 | 98 |
| 学生 | 平均数 | 中位数 | 众数 | 方差 |
| 甲 | 98 | 99 | 99 | 4.4 |
| 乙 | 93 | 93 | 93 | 2.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
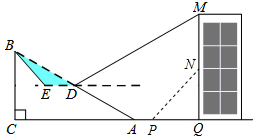 如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com