
【题目】如图①,在![]() 中,
中, ![]() ,
, ![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() 、
、![]() .直线
.直线![]() 、
、![]() 交于点
交于点![]() .
.
(![]() )当
)当![]() 时,
时, ![]() __________.
__________.
(![]() )在旋转过程中,四边形
)在旋转过程中,四边形![]() 的面积是否存在最大值?若存在,求出最大值.若不存在,说明理由.
的面积是否存在最大值?若存在,求出最大值.若不存在,说明理由.
(![]() )如图②.若
)如图②.若![]() 中,
中, ![]() ,其余条件不变,四边形
,其余条件不变,四边形![]() 的面积是否存在最大值?若存,求出最大值.若不存在,说明理由.
的面积是否存在最大值?若存,求出最大值.若不存在,说明理由.

【答案】(1)![]() ;(
;(![]() )存在,理由见解析;(
)存在,理由见解析;(![]() )存在,理由见解析.
)存在,理由见解析.
【解析】试题分析:(1)根据等腰三角形两底角相等,即可解决问题.
(2)存在.首先证明∠AMC=90°,在Rt△ABC中,根据AB=4,BC=3,可得![]() ,可得S△ABC=
,可得S△ABC=![]() ×3×4=6,因为当△ACM的面积最大时,四边形ABCM的面积最大,因为△ACM是直角三角形,AC=5,所以当AM=CM=
×3×4=6,因为当△ACM的面积最大时,四边形ABCM的面积最大,因为△ACM是直角三角形,AC=5,所以当AM=CM=![]() 时,△ACM的面积最大,最大值为=
时,△ACM的面积最大,最大值为=![]() ,由此即可解决问题.
,由此即可解决问题.
(3)存在.如图②中,作AN⊥BC于N.首先证明∠AMC=60°,在Rt△ABN中,AB=4,∠ABN=60°,推出BN=![]() AB=2,AN=
AB=2,AN=![]() ,在Rt△ACN中,
,在Rt△ACN中, ![]() ,可得S△ABC=
,可得S△ABC=![]() ×3×2=
×3×2=![]() ,因为当△ACM的面积最大时,四边形ABCM的面积最大,因为∠AMC=60°所以当△ACM是等边三角形时,△ACM的面积最大,由此即可解决问题.
,因为当△ACM的面积最大时,四边形ABCM的面积最大,因为∠AMC=60°所以当△ACM是等边三角形时,△ACM的面积最大,由此即可解决问题.
解:(![]() )∵
)∵![]() ,
, ![]() ,
,
∴![]() .
.
故答案为![]() .
.
(![]() )存在,理由如下,
)存在,理由如下,
如图①中,
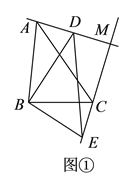
∵![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴当![]() 的面积最大时,四边形
的面积最大时,四边形![]() 的面积最大,
的面积最大,
∵![]() 是直角三角形,
是直角三角形, ![]() ,
,
∴当![]() 时,
时, ![]() 的面积最大,最大值为
的面积最大,最大值为![]() ,
,
∴四边形![]() 的面积的最大值为
的面积的最大值为![]() .
.
(![]() )存在,理由如下,
)存在,理由如下,
如图②中,作![]() 于
于![]() ,
,
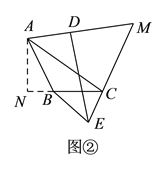
∵![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴当![]() 的面积最大时,四边形
的面积最大时,四边形![]() 的面积最大,
的面积最大,
∵![]() ,
,
∴当![]() 是等边三角形时,
是等边三角形时, ![]() 的面积最大,
的面积最大,
最大值为![]() ,
,
∴四边形![]() 的面积的最大值为
的面积的最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 分别为
分别为![]() 边上的动点.
边上的动点.
(1)若点![]() 分别为
分别为![]() 的中点,求线段
的中点,求线段![]() 的长;
的长;
(2)若![]() ,
,
①求证: ![]() ∽
∽![]() ;
;
②试问![]() 与
与![]() 相似吗?并说明理由.
相似吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.
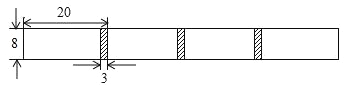
![]() 根据题意,将下面的表格补充完整:
根据题意,将下面的表格补充完整:
白纸张数 | 1 | 2 | 3 | 4 | 5 |
|
纸条长度 | 20 | ______ | 54 | 71 | ______ |
|
![]() 直接写出用x表示y的关系式:______ ;
直接写出用x表示y的关系式:______ ;
![]() 要使粘合后的总长度为1006cm,需用多少张这样的白纸?
要使粘合后的总长度为1006cm,需用多少张这样的白纸?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是 .
(2)请用列表法或画树状图法求小明和小亮诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,分别探索下列四个图形中∠P、∠A、∠C,发现有如下三种数量关系:∠A+∠C =∠P ;∠P+∠A =∠C ;∠P+∠C =∠A,请你选择其中的两种数量关系说明理由.
(1)我选择的是图 ,数量关系式是 .
理由:
(2) 我选择的是图 ,数量关系式是 .
理由:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 半径为
半径为![]() ,
, ![]() 是⊙
是⊙![]() 的直径,
的直径, ![]() 是⊙
是⊙![]() 上一点,连接
上一点,连接![]() ,⊙
,⊙![]() 外的一点
外的一点![]() 在直线
在直线![]() 上.
上.
(![]() )若
)若![]() ,
, ![]() .
.
①求证: ![]() 是⊙
是⊙![]() 的切线.
的切线.
②阴影部分的面积是__________.(结果保留![]() )
)
(![]() )当点
)当点![]() 在⊙
在⊙![]() 上运动时,若
上运动时,若![]() 是⊙
是⊙![]() 的切线,探究
的切线,探究![]() 与
与![]() 的数量关系.
的数量关系.
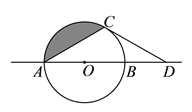
查看答案和解析>>
科目:初中数学 来源: 题型:
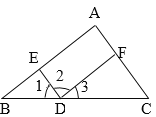
【题目】如图7,推理填空:
(1)∵∠A =∠_____(已知),
∴AC∥ED(____________________________________);
(2)∵∠2 =∠_____(已知),
∴AC∥ED(_________________________________________);
(3)∵∠A +∠____ = 180°(已知),
∴AB∥FD(_________________________________________);
(4)∵AC∥ED(已知),
∴∠2 +∠____ = 180°(_________________________________________);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.

(1)根据题意,将下面的表格补充完整.
白纸张数x(张) | 1 | 2 | 3 | 4 | 5 | … |
纸条总长度y(cm) | 20 | 54 | 71 | … |
(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com