
【题目】如图,⊙![]() 是
是![]() 的内切圆,切点分别为
的内切圆,切点分别为![]() 、
、![]() 、
、![]() ,
, ![]() ,
, ![]() .
.
(![]() )求
)求![]() 的度数.
的度数.
(![]() )求
)求![]() 的度数.
的度数.
【答案】(![]() )
)![]() (
(![]() )
)![]()
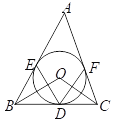
【解析】试题分析:(1)由切线长定理可知BO,CO分别是∠ABC和∠ACB的角平分线,则∠OBC和∠OCB的度数可求出,进而可求出∠BOC的度数;
(2)连接OE,OF.由三角形内角和定理可求得∠A=50°,由切线的性质可知:∠OFA=90°,∠OEA=90°,从而得到∠A+∠EOF=180°,故可求得∠EOF=130°由圆周角定理可求得∠EDF=65°.
试题解析:解:(1)∵⊙O是△ABC的内切圆,切点分别为D、E、F,∴BO,CO分别是∠ABC和∠ACB的角平分线,∴∠OBC=![]() ∠ABC=30°,∠OCB=
∠ABC=30°,∠OCB=![]() ∠ACB=35°,∴∠BOC=180°﹣30°﹣35°=115°;
∠ACB=35°,∴∠BOC=180°﹣30°﹣35°=115°;
(2)如图所示;连接OE,OF.
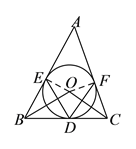
∵∠ABC=60°,∠ACB=70°,∴∠A=180°﹣60°﹣70°=50°.
∵AB是圆O的切线,∴∠OFA=90°.
同理∠OEA=90°,∴∠A+∠EOF=180°,∴∠EOF=130°,∴∠EDF=65°.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本
(1)求每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.已知:在矩形![]() 中,
中,![]() 是对角线,
是对角线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ;
;
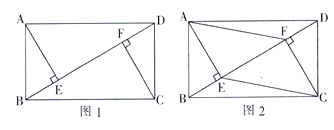
(1)如图1,求证:![]() ;
;
(2)如图2,当![]() 时,连接
时,连接![]() .
.![]() ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形![]() 面积的
面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共435人参加一次大型公益活动,如果租用5辆小客车和6辆大客车恰好全部坐满,已知每辆大客车的乘客座位数比小客车多12个.
(1) 求每辆小客车和每辆大客车的乘客座位数;
(2) 由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中, ![]() ,
, ![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() 、
、![]() .直线
.直线![]() 、
、![]() 交于点
交于点![]() .
.
(![]() )当
)当![]() 时,
时, ![]() __________.
__________.
(![]() )在旋转过程中,四边形
)在旋转过程中,四边形![]() 的面积是否存在最大值?若存在,求出最大值.若不存在,说明理由.
的面积是否存在最大值?若存在,求出最大值.若不存在,说明理由.
(![]() )如图②.若
)如图②.若![]() 中,
中, ![]() ,其余条件不变,四边形
,其余条件不变,四边形![]() 的面积是否存在最大值?若存,求出最大值.若不存在,说明理由.
的面积是否存在最大值?若存,求出最大值.若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校决定对初三学生进行体育成绩测试,成绩记入总分,同学们将根据自己平时的运动成绩确定自己的参考项目,下面是小亮同学的两个项目立定跳远和一分钟跳绳在近期连续五次测试的得分情况(立定跳远得分统计表和一分钟跳绳得分折线图):
立定跳远得分统计表
测试 日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
得分 | 7 | 10 | 8 | 9 | 6 |
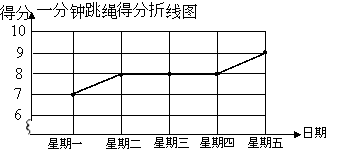
(1)请根据以上信息,分别将这两个项目的平均数、极差、方差填入下表:
统计量 | 平均数 | 极差 | 方差 |
立定跳远 | 8 | ||
一分钟跳绳 | 2 | 0.4 |
(2)根据以上信息,你认为在立定跳远和一分钟跳绳这两个项目中,小亮应选择哪个项目作为体育考试的参考项目?请简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
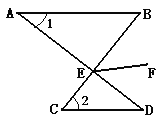
【题目】如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=300,∠2=400。(1)求∠B、∠D的度数.(2)求∠BEF的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,下列条件中,不能使四边形DBCE成为菱形的是( )

A.AB=BEB.BE⊥DCC.∠ABE=90°D.BE平分∠DBC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com