【题目】一个袋中装有除颜色外都相同的红球和黄球共10个，其中红球6个．从袋中任意摸出1球．
（1）“摸出的球是白球”是什么事件？它的概率是多少？
（2）“摸出的球是黄球”是什么事件？它的概率是多少？
名校课堂系列答案科目：初中数学 来源： 题型：
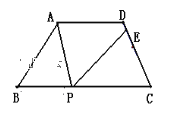
【题目】如图，等腰梯形ABCD中，AD∥BC，AD=3，BC=7，∠B=60°，P为下底BC上一点（不与B、C重合），连结AP，过点P作PE交CD于E，使得∠APE=∠B
（1）求证：△ABP∽△PCE
（2）在底边BC上是否存在一点P，使DE：EC=5：3？如果存在，求BP的长；如果不存在，请说明理由
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，山上有一座高塔，山脚下有一圆柱形建筑物平台，高塔及山的剖面与圆柱形建筑物平台的剖面ABCD在同一平面上，在点A处测得塔顶H的仰角为35°，在点D处测得塔顶H的仰角为45°，又测得圆柱形建筑物的上底面直径AD为6m，高CD为2.8m，则塔顶端H到地面的高度HG为（ ）
（参考数据：
，
，
，
）
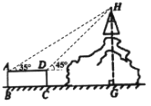
A.10.8mB.14mC.16.8mD.29.8m
查看答案和解析>>
科目：初中数学 来源： 题型：
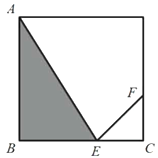
【题目】某人定制了一批地砖，每块地砖（如图（1）所示）是边长为0.5米的正方形
．点E、F分别在边
和
上，
、
和四边形
均由单一材料制成，制成
、和四边形的三种材料的价格依次为每平方米30元、20元、10元．若将此种地砖按图（2）所示的形式铺设，且中间的阴影部分组成正方形
．设
．
（1）
________，
_________．（用含有x的代数式表示）．
（2）已知烧制该种地砖平均每块需加工费0.35元，若要
长大于0.1米，且每块地砖的成本价为4元（成本价=材料费用+加工费用），则长应为多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题：（1）如图①，在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，则线段BC，DC，EC之间满足的等量关系式为 ；
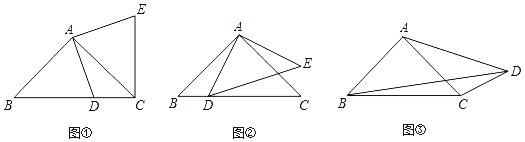
探索：（2）如图②，在Rt△ABC与Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；
应用：（3）如图③，在四边形ABCD中，∠ABC＝∠ACB＝∠ADC＝45°．若BD＝9，CD＝3，求AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y＝
x2+bx+3的对称轴为直线x＝1．若关于x的一元二次方程x2+bx+3﹣t＝0（t为实数）在﹣2＜x＜3的范围内有实数根，则t的取值范围是（ ）
A.12＜t≤3B.12＜t＜4C.12＜t≤4D.12＜t＜3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的边长为4，点E是CD的中点，AF平分∠BAE交BC于点F，将△ADE绕点A顺时针旋转90°得△ABG，则CF的长为____.
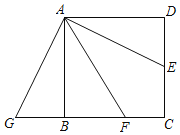
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(9分)已知：
ABCD的两边AB，AD的长是关于x的方程
的两个实数根．
（1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；
（2）若AB的长为2，那么ABCD的周长是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
