
如图,在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,∠ADB=∠CAD+∠ABD,∠BAD=3∠CBD.
(1)求证:△ABC为等腰三角形;
(2)M是线段BD上一点,BM:AB=3:4,点F在BA的延长线上,连接FM,∠BFM的平分线FN交BD于点N,交AD于点G,点H为BF中点,连接MH,当GN=GD时,探究线段CD、FM、MH之间的数量关系,并证明你的结论.
(1)见解析;(2)2MH=FM+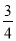 CD.见解析
CD.见解析
【解析】
试题分析:(1)由等式的性质,可得∠APE=∠ADE,由等腰三角形的性质,可得∠PAD=2β,由直角三角形的性质,可得∠AEB+∠CBE=90°,由等式的性质,可得∠ABC=∠ACB,再由等腰三角形的判定,可得答案;
(2)由相似三角形的判定与性质,可得∠ABE=∠ACD,由等腰三角形的性质,可得∠GND=∠GDN,由对顶角的性质,可得∠AGF的度数,由三角形外角的性质,∠AFG的度数,由直角三角形的性质,可得BF与MH的关系,由等腰三角形的性质,可得∠FRM=∠FMR,由平行线的判定与性质,可得∠CBD=∠RMB,由相似三角形的判定与性质,可得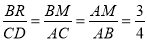 ,由线段的和差,可得BR=BF﹣FR,再由等量代换,可得答案.
,由线段的和差,可得BR=BF﹣FR,再由等量代换,可得答案.
试题解析:(1)如图1,作∠BAP=∠DAE=β,AP交BD于P,
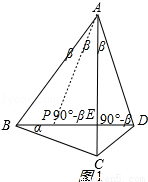
设∠CBD=α,∠CAD=β,
∵∠ADB=∠CAD+∠ABD,∠APE=∠BAP+∠ABD,
∴∠APE=∠ADE,AP=AD.
∵AC⊥BD
∴∠PAE=∠DAE=β,
∴∠PAD=2β,∠BAD=3β.
∵∠BAD=3∠CBD,
∴3β=3α,β=α.
∵AC⊥BD,
∴∠ACB=90°﹣∠CBE=90°﹣α=90°﹣β.
∵∠ABC=180°﹣∠BAC﹣∠ACB=90°﹣β,
∴∠ACB=∠ABC,
∴△ABC为等腰三角形;
(2)2MH=FM+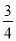 CD.
CD.
如图2,
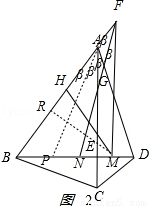
由(1)知AP=AD,AB=AC,∠BAP=∠CAD=β,
∴△ABP∽△ACD,
∴∠ABE=∠ACD.
∵AC⊥BD,
∴∠GDN=90°﹣β,
∵GN=GD,
∴∠GND=∠GDN=90°﹣β,
∴∠NGD=180°﹣∠GND﹣∠GDN=2β.
∴∠AGF=∠NGD=2β.
∴∠AFG=∠BAD﹣∠AGF=3β﹣2β=β.
∵FN平分∠BFM,
∴∠NFM=∠AFG=β,
∴FM∥AE,
∴∠FMN=90°.
∵H为BF的中点,
∴BF=2MH.
在FB上截取FR=FM,连接RM,
∴∠FRM=∠FMR=90°﹣β.
∵∠ABC=90°﹣β,
∴∠FRM=∠ABC,
∴RM∥BC,
∴∠CBD=∠RMB.
∵∠CAD=∠CBD=β,
∴∠RMB=∠CAD.
∵∠RBM=∠ACD,
∴△RMB∽△DAC,
∴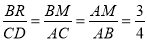 ,
,
∴BR=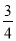 CD.
CD.
∵BR=BF﹣FR,
∴FB﹣FM=BR=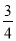 CD,
CD,
FB=FM+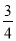 CD.
CD.
∴2MH=FM+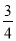 CD.
CD.
考点:1、等腰三角形的性质与判定;2、直角三角形的性质;3、相似三角形的判定与性质;4、直角三角形的性质


科目:初中数学 来源:2014年初中毕业升学考试(黑龙江大庆卷)数学(解析版) 题型:填空题
某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为 人.(注:横轴上每组数据包含最小值不包含最大值)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江大庆卷)数学(解析版) 题型:选择题
下列四个命题:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形;
(4)一组对边平行且相等的四边形是平行四边形.
其中正确的命题个数有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江哈尔滨卷)数学(解析版) 题型:解答题
君畅中学计划购买一些文具送给学生,为此学校决定围绕“在笔袋、圆规、直尺、钢笔四种文具中,你最需要的文具是什么?(必选且只选一种)”的问题,在全校满园内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据以上信息回答下列问题:
(1)在这次调查中,最需要圆规的学生有多少名?并补全条形统计图;
(2)如果全校有970名学生,请你估计全校学生中最需要钢笔的学生有多少名?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江哈尔滨卷)数学(解析版) 题型:填空题
在一个不透明的口袋中,有四个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸取一个小球记下标号后放回,再随机地摸取一个小球记下标号,则两次摸取的小球标号都是1的概率为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(青海西宁卷)数学(解析版) 题型:解答题
今年5月1日起实施《青海省保障性住房准入分配退出和运营管理实施细则》规定:公共租赁住房和廉租住房并轨运行(以下简称并轨房),计划10年内解决低收入人群住房问题.已知第x年(x为正整数)投入使用的并轨房面积为y百万平方米,且y与x的函数关系式为y=- x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
时间x(单位:年,x为正整数) | 1 | 2 | 3 | 4 | 5 | … |
单位面积租金z(单位:元/平方米) | 50 | 52 | 54 | 56 | 58 |
|
(1)求出z与x的函数关系式;
(2)设第x年政府投入使用的并轨房收取的租金为W百万元,请问政府在第几年投入使用的并轨房收取的租金最多,最多为多少百万元?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(重庆A卷)数学(解析版) 题型:选择题
如图,反比例函数 在第二象限的图象上有两点A、B,它们的横坐标分别为-1,-3.直线AB与x轴交于点C,则△AOC的面积为( )
在第二象限的图象上有两点A、B,它们的横坐标分别为-1,-3.直线AB与x轴交于点C,则△AOC的面积为( )
A.8 B.10 C.12 D.24

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com