
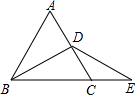
 如图,等边△ABC的周长是12,D是AC边上的中点,E在BC的延长线上,若DE=DB,则CE的长为2.
如图,等边△ABC的周长是12,D是AC边上的中点,E在BC的延长线上,若DE=DB,则CE的长为2. 分析 由△ABC为等边三角形,且BD为边AC的中线,根据“三线合一”得到BD平分∠ABC,而∠ABC为60°,得到∠DBE为30°,又因为DE=DB,根据等边对等角得到∠E与∠DBE相等,故∠E也为30°;
由等边三角形的三边相等且周长为9,求出AC的长为3,且∠ACB为60°,根据∠ACB为△DCE的外角,根据三角形的外角等于与它不相邻的两个内角之和,求出∠CDE也为30°,根据等角对等边得到CD=CE,都等于边长AC的一半,从而求出CE的值.
解答 解:∵△ABC为等边三角形,D为AC边上的中点,
∴BD为∠ABC的平分线,且∠ABC=60°,
即∠DBE=30°,又DE=DB,
∴∠E=∠DBE=30°,
∵等边△ABC的周长为9,
∴AC=3,且∠ACB=60°,
∴∠CDE=∠ACB-∠E=30°,即∠CDE=∠E,
∴CD=CE=$\frac{1}{2}$AC=2.
故答案为:2.
点评 此题考查了等边三角形的性质,利用等边三角形的性质可以解决角与边的有关问题,尤其注意等腰三角形“三线合一”性质的运用,及“等角对等边”、“等边对等角”的运用.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10πcm2 | B. | 20πcm2 | C. | 40πcm2 | D. | 80πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有理数a、b、c在数轴上的位置大致如下:
如图,有理数a、b、c在数轴上的位置大致如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从O点开始沿OA边向点A以1cm/s的速度移动,点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P、Q同时出发,用t(单位:秒)表示移动的时间(0≤t≤6),那么:
如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从O点开始沿OA边向点A以1cm/s的速度移动,点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P、Q同时出发,用t(单位:秒)表示移动的时间(0≤t≤6),那么:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com