
【题目】已知函数y =(2m+1) x+ m-3
(1) 若函数图象经过原点,求m的值.
(2) 若函数图象在y轴的交点的纵坐标为-2,求m的值.
(3)若函数的图象平行直线y=-3x–3,求m的值.
(4)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
【答案】(1)m=3;(2)m=1;(3)m=-2;(4)m<-![]() .
.
【解析】
试题(1)若函数图象经过原点,m-3=0,解得m=3.
(2)依题意知,当x=0时,y=(2m+1) x+ m-3=-2。解得:m=1.
(3)依题意知,函数y ="(2m+1)" x+ m-3平行于直线y=3x–3,设函数y ="(2m+1)" x+ m-3为直线y=3x–3上下平移所得平行线,设x=1时,则y=3m-2,即(1,3m-2),x=0时,y=m-3,即(0,m-3)而直线y=3x–3则经过(1,0)(0,-3)可得m-3-(-3)=3m-2,解得m=1.
(4)若这个函数是一次函数,且y随着x的增大而减小,可知k<0,2m+1<0.解得m<![]() 。
。


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量? 操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现定义新运算“△”,对于任意有理数a,b,都有a△b=a2-ab+b,例如:3△5=32-3×5+5=-1,请根据上述知识解决问题:
(1)化简:(x-1)△(2+x);
(2)若(1)中的代数式的值大于6而小于9,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如图1,将n个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax2+bx+c(a<0)过矩形顶点B、C. 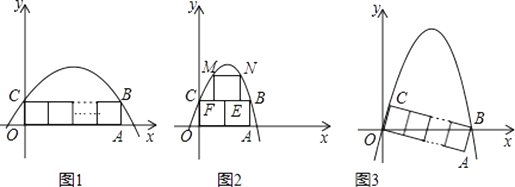
(1)当n=1时,如果a=﹣1,试求b的值;
(2)当n=2时,如图2,在矩形OABC上方作一边长为1的正方形EFMN,使EF在线段CB上,如果M,N两点也在抛物线上,求出此时抛物线的解析式;
(3)将矩形OABC绕点O顺时针旋转,使得点B落到x轴的正半轴上,如果该抛物线同时经过原点O. ①试求当n=3时a的值;
②直接写出a关于n的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
A.如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是 ;
B.用科学计算器计算:![]() sin58°≈(精确到0.01).
sin58°≈(精确到0.01).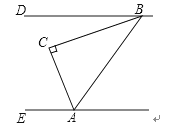
查看答案和解析>>
科目:初中数学 来源: 题型:
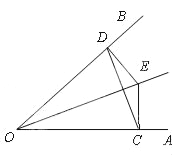
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C、D.
(1)请判断△EDC的形状并说明理由;
(2)求证OE是线段CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B两种型号的学习用品共1000件,已知A型学习用品的单价为20元,B型学习用品的单价为30元.
(1)若购买这批学习用品用了26000元,则购买A,B两种学习用品各多少件?
(2)若购买这批学习用品的钱不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
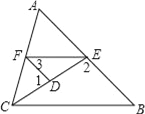
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com