
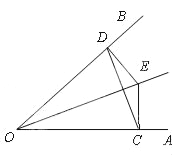
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C、D.
(1)请判断△EDC的形状并说明理由;
(2)求证OE是线段CD的垂直平分线.
【答案】(1)解△EDC是等腰三角形,理由见解析;(2)见解析.
【解析】
(1)根据角平分线性质得出DE=EC,即可得出答案;
(2)证△EDO和△ECO全等,推出OD=OC,根据线段垂直平分线性质得出即可.
(1)解:△EDC是等腰三角形,
理由是:
∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D,
∴DE=CE,
∴△EDC是等腰三角形;
(2)证明:∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D,
∴DE=CE,∠EDO=∠ECO=90°,
在Rt△ODE与Rt△OCE中,
![]()
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∵DE=EC,
∴OE是线段CD的垂直平分线.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示. 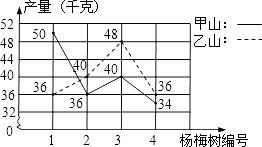
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y =(2m+1) x+ m-3
(1) 若函数图象经过原点,求m的值.
(2) 若函数图象在y轴的交点的纵坐标为-2,求m的值.
(3)若函数的图象平行直线y=-3x–3,求m的值.
(4)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
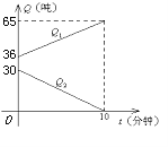
【题目】某军加油飞机接到命令,立即给另一架正在飞行的运输飞机进行空中加油.在加油的过程中,设运输飞机的油箱余油量为Q1吨,加油飞机的加油油箱的余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数关系如图.回答问题:
(1) 加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需要多少分钟?
(2) 求加油过程中,运输飞机的余油量Q1(吨)与时间t(分钟)的函数关系式;
(3) 运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用?
请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线 y=kx+b 与直线![]() 交点的纵坐标为 5,而与直线 y=3x﹣9 的交点的横 坐标也是 5,则直线 y=kx+b 与两坐标轴围成的三角形面积为( )
交点的纵坐标为 5,而与直线 y=3x﹣9 的交点的横 坐标也是 5,则直线 y=kx+b 与两坐标轴围成的三角形面积为( )
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样大小的灰、白两种正方形地砖铺设地面,方法是(如图):第一层只有2块白色地砖,第二层是在第一层外面围一圈灰色地砖,第三层是在第二层外面围一圈白色地砖……
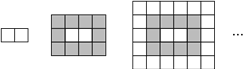
(1)第七层共有几块地砖,是白色的还是灰色的?
(2)第n层共有几块地砖(结果化成最简)?如果这些地砖是白色的,那么正整数n有什么特点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE.
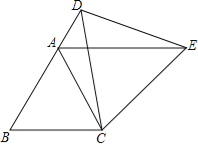
(1)求证:△CBD≌△CAE.
(2)判断AE与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实践中学习:
(1)如图1所示:已知AB∥CD,∠ABD=115°,根据 可得出:∠BDC的度数是 .
(2)如图2所示:已知AB∥CD,∠ABC=25°,∠EDC=40°,求∠BED的度数.
(3)如图3所示:已知MA∥NC,试确定∠A、∠B、∠C和∠E、∠F的关系,并说明理由.
(4)如图4所示:已知AB∥CD,∠ABE=α,∠FCD=β,∠CFE=γ,且BE⊥EF,试确定α、β、γ的关系,请说明理由.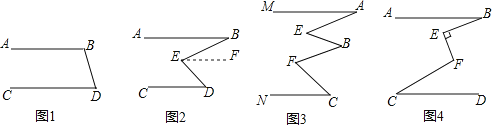
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com