
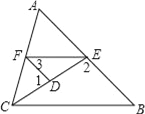
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
【答案】(1)详见解析;(2)70°.
【解析】
(1)求出DF∥AB,推出∠3=∠AEF,求出∠B=∠AEF,得出FE∥BC,根据平行线性质求出即可;
(2)求出∠FED=80°-45°=35°,根据平行线性质求出∠BCE=∠FED=35°,求出∠ACB=2∠BCE=70°,根据平行线性质求出即可.
解:(1)因为∠1+∠FDE=180°,∠1,∠2互为补角,
所以∠2=∠FDE,所以DF∥AB,所以∠3=∠AEF.
因为∠3=∠B,所以∠B=∠AEF,所以FE∥BC,
所以∠AFE=∠ACB.
(2)因为∠1=80°,所以∠FDE=180°-∠1=100°.
因为∠3+∠FDE+∠FED=180°,
所以∠FED=180°-∠FDE-∠3=35°.
因为EF∥BC,所以∠BCE=∠FED=35°.
因为CE平分∠ACB,
所以∠ACB=2∠BCE=70°,
所以∠AFE=∠ACB=70°.


科目:初中数学 来源: 题型:
【题目】已知函数y =(2m+1) x+ m-3
(1) 若函数图象经过原点,求m的值.
(2) 若函数图象在y轴的交点的纵坐标为-2,求m的值.
(3)若函数的图象平行直线y=-3x–3,求m的值.
(4)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE.
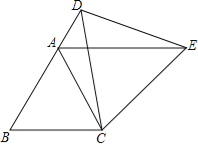
(1)求证:△CBD≌△CAE.
(2)判断AE与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程:①y=4x+2,②2x-3y=4.
(1)根据方程①填写下表:
x | 2 | 1 | 0 | -1 | -2 |
y |
(2)根据方程②填写下表:
x | 2 | 1 | 0 | -1 | -2 |
y |
(3)根据以上两表中的数据,求方程组![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):

①接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
②若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
③若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字﹣1、1、2.随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实践中学习:
(1)如图1所示:已知AB∥CD,∠ABD=115°,根据 可得出:∠BDC的度数是 .
(2)如图2所示:已知AB∥CD,∠ABC=25°,∠EDC=40°,求∠BED的度数.
(3)如图3所示:已知MA∥NC,试确定∠A、∠B、∠C和∠E、∠F的关系,并说明理由.
(4)如图4所示:已知AB∥CD,∠ABE=α,∠FCD=β,∠CFE=γ,且BE⊥EF,试确定α、β、γ的关系,请说明理由.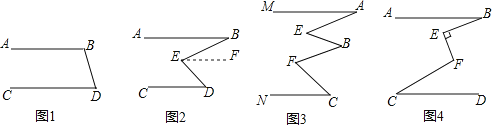
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E.若OD=8,OP=10,则PE的长为( ) 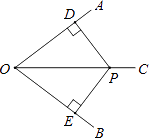
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4),
(1)将△ABC各顶点的横坐标保持不变,纵坐标分别减5后得到△A1B1C1;
①请在图中画出△A1B1C1;
②求这个变换过程中线段AC所扫过的区域面积;
(2)将△ABC绕点(1,0)按逆时针方向旋转90°后得到的△A2B2C2,请在图中画出△A2B2C2,并分别写出△A2B2C2的顶点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com