
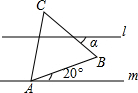
 如图,l∥m,等边△ABC的顶点A在m上,则∠α的度数为( )
如图,l∥m,等边△ABC的顶点A在m上,则∠α的度数为( )| A. | 20° | B. | 40° | C. | 50° | D. | 60° |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
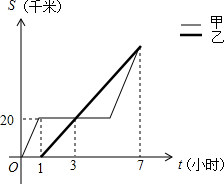 甲、乙两人骑自行车分别从A地出发,沿同一路线去B地,甲先行1小时到达距离A地20千米的C地,甲因事耽误一会儿,事后继续按原速行驶,并与乙同时到达B地,如图表示甲、乙两人骑自行车行驶的路程S(千米)岁时间t(小时)变化图象(全程),据图象回答下列问题:
甲、乙两人骑自行车分别从A地出发,沿同一路线去B地,甲先行1小时到达距离A地20千米的C地,甲因事耽误一会儿,事后继续按原速行驶,并与乙同时到达B地,如图表示甲、乙两人骑自行车行驶的路程S(千米)岁时间t(小时)变化图象(全程),据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
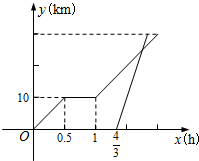 周末,小明骑电动自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑电动自行车速度的3倍.
周末,小明骑电动自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑电动自行车速度的3倍.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<c<a | C. | a<c<b | D. | b<a<c |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com