

分析 (1)连接PM,PN,由切线的性质得PM⊥MF,PN⊥ON,由P(1,1)得PM=PN,利用全等三角形的判定定理得△PMF≌△PNE,得出结论PF=PE.
(2))利用分类讨论的思想,①当t>1时,点E在y轴的负半轴上,利用(1)中的结论,由全等三角形的性质得,NE=MF=t,PM=PN=1,数形结合用t分别表示OE=a,OF=b,消去t可得a,b的关系;②0<t≤1时,点E在y轴的正半轴或原点上,同理可证△PMF≌△PNE,数形结合用t分别表示OE=a,OF=b,消去t可得a,b的关系;
(3)由点对称的性质得F(1+t,0),F′(1-t,0),由经过M、E和F′三点的抛物线的对称轴交x轴于点Q得Q(1-$\frac{1}{2}$t,0),OQ=1-$\frac{1}{2}$t,由△PMF≌△PNE得NE=MF=t,OE=t-1,利用相似三角形的性质分类讨论得出结论.
解答 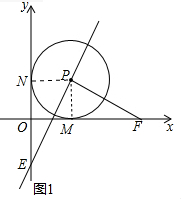 (1)证明:如图1,连接PM,PN,
(1)证明:如图1,连接PM,PN,
∵⊙P与x轴,y轴分别相切于点M和点N,
∴PM⊥MF,PN⊥ON且PM=PN
∴∠PMF=∠PNE=90°且∠NPM=90°
∵PE⊥PF,∠NPE=∠MPF=90°-∠MPE
在△PMF和△PNE中,
$\left\{\begin{array}{l}{∠NPE=∠MPF}\\{PN=PM}\\{∠PNE=∠PMF}\end{array}\right.$,
∴△PMF≌△PNE(SAS),
∴PE=PF.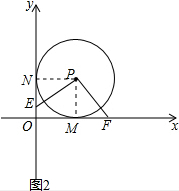
(2)①当t>1时,点E在y轴的负半轴上,如图1,
由(1)得△PMF≌△PNE,
∴NE=MF=t,PM=PN=1,
∴b=OF=OM+MF=1+t,a=OE=NE-ON=t-1,
∴b-a=1+t-(t-1)=2,
∴b=2+a,
②0<t≤1时,点E在y轴的正半轴或原点上,如图2,
同理可证△PMF≌△PNE
∴b=OF=OM+MF=1+t,a=ON-NE=1-t,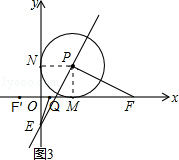
∴b+a=1+t+1-t=2,∴b=2-a;
(3)如图3或图4,当1<t<2时,
∵F(1+t,0),F和F′关于点M对称,
∴F′(1-t,0),
∵经过M、E和F′三点的抛物线的对称轴交x轴于点Q,
∴Q(1-$\frac{1}{2}$t,0),
∴OQ=1-$\frac{1}{2}$t,
由(1)得△PMF≌△PNE,
∴NE=MF=t,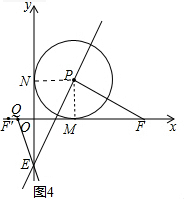
∴OE=t-1,
当△OEQ∽△MPF时,$\frac{OE}{OP}=\frac{OQ}{MF}$,
∴$\frac{t-1}{1}=\frac{1-\frac{1}{2}t}{t}$,
∴t=$\frac{1+\sqrt{17}}{4}$,
当△OEQ∽△MFP时,$\frac{OE}{MF}=\frac{OQ}{MP}$,
∴$\frac{t-1}{t}=\frac{1-\frac{1}{2}t}{1}$,
∴t=$\sqrt{2}$,
∴当t=$\frac{1+\sqrt{17}}{4}$,或t=$\sqrt{2}$时,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似.
点评 本题主要考查了切线定理,全等三角形的性质与判定,相似三角形的性质,利用数形结合,分类讨论的思想是解答此题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:选择题
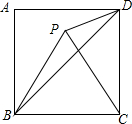 如图,已知正方形ABCD的边长为2,以C点为圆心将线段BC顺时针旋转60°,连接BP.PD,则PD的长是( )
如图,已知正方形ABCD的边长为2,以C点为圆心将线段BC顺时针旋转60°,连接BP.PD,则PD的长是( )| A. | $\sqrt{7-4\sqrt{3}}$ | B. | 2-$\sqrt{3}$ | C. | $\sqrt{3}$-2 | D. | $\sqrt{8-4\sqrt{3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1的平方根是±1 | B. | -1的立方根是-1 | ||
| C. | $\sqrt{2}$是2的一个平方根 | D. | -3是$\sqrt{(-3)^{2}}$的一个平方根 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com