考点:解直角三角形
专题:分类讨论
分析:过A作AD⊥BC于D,分为两种情况,画出图形,求出∠BAD和∠CAD,即可求出答案.
解答: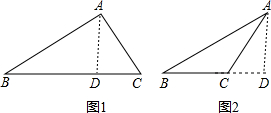
解:过A作AD⊥BC于D,
分为两种情况:①如图1,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠B=30°,AB=2,
∴AD=1,∠BAD=60°,
∵AC=
,
∴由勾股定理得:CD=
=1=AD,
∴∠CAD=∠ACD=45°,
∴∠BAC=60°+45°=105°;
②如图2,∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠B=30°,AB=2,
∴AD=1,∠BAD=60°,
∵AC=
,
∴由勾股定理得:CD=
=1=AD,
∴∠CAD=∠ACD=45°,
∴∠BAC=60°-45°=15°;
故答案为:105°或15°.
点评:本题咔嚓了解直角三角形,勾股定理的应用,主要考查学生的计算能力,用了分类讨论思想.




 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案