
【题目】某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取5次,记录如下:
甲 | 85 | 88 | 84 | 85 | 83 |
乙 | 83 | 87 | 84 | 86 | 85 |
(1)请你分别计算这两组数据的平均数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
【答案】(1)甲平均数: 85,乙平均数: 85;(2)选派乙工人参加合适,理由见解析;
【解析】
(1)根据平均数的概念列式计算即可得解;
(2)求出两人测试成绩的方差,然后根据方差越小越稳定选择合适人选.
解:(1)甲平均数:![]() ×(85+88+84+85+83)=
×(85+88+84+85+83)=![]() ×425=85,
×425=85,
乙平均数:![]() ×(83+87+84+86+85)=
×(83+87+84+86+85)=![]() ×425=85;
×425=85;
(2)选派乙工人参加合适.
理由如下:S甲2=![]() ×[(85﹣85)2+(88﹣85)2+(84﹣85)2+(85﹣85)2+(83﹣85)2],
×[(85﹣85)2+(88﹣85)2+(84﹣85)2+(85﹣85)2+(83﹣85)2],
=![]() ×(0+9+1+0+4),
×(0+9+1+0+4),
=2.8,
S乙2=![]() ×[(83﹣85)2+(87﹣85)2+(84﹣85)2+(86﹣85)2+(85﹣85)2],
×[(83﹣85)2+(87﹣85)2+(84﹣85)2+(86﹣85)2+(85﹣85)2],
=![]() ×(4+4+1+1+0),
×(4+4+1+1+0),
=2,
∵2.8>2,
∴S甲2>S乙2,
∴乙成绩更稳定,
∴选派乙工人参加合适.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
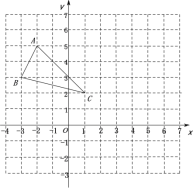
【题目】如图,在平面直角坐标系中,已知点A(-2,5),B(-3,3),C(1,2),点P(m,n)是三角形ABC内任意一点,三角形经过平移后得到三角形A1B1C1,点P的对应点为P1(m+6,n-2).
(1)直接写出平移后点A1、B1、C1的坐标分别为 .
(2)画出三角形ABC平移后的三角形A1B1C1..
查看答案和解析>>
科目:初中数学 来源: 题型:
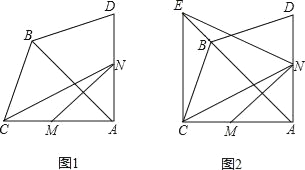
【题目】如图1,在△ABC中,AB=AC=4,∠ABC=67.5°,△ABD和△ABC关于AB所在的直线对称,点M为边AC上的一个动点(重合),点M关于AB所在直线的对称点为N,△CMN的面积为S.
(1)求∠CAD的度数;
(2)设CM=x,求S与x的函数表达式,并求x为何值时S的值最大?
(3)S的值最大时,过点C作EC⊥AC交AB的延长线于点E,连接EN(如图2),P为线段EN上一点,Q为平面内一点,当以M,N,P,Q为顶点的四边形是菱形时,请直接写出所有满足条件NP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
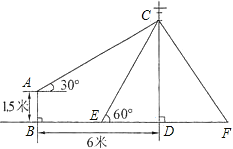
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
(1)如图①,若 0°<α<90°,当 AD′∥CE′时,求α的大小;
(2)如图②,若 90°<α<180°,当点 D′落在线段 BE′上时,求 sin∠CBE′的值;
(3)若直线AD′与直线BE′相交于点P,求点P的横坐标m的取值范围(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
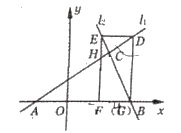
【题目】如图,已知直线![]() :
:![]() 与直线
与直线![]() :
:![]() 相交于点
相交于点![]() ,直线
,直线![]() 、
、![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点,矩形
两点,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,顶点
上,顶点![]() 、
、![]() 都在
都在![]() 轴上,且点
轴上,且点![]() 与
与![]() 点重合,那么
点重合,那么![]() __________________.
__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,E,F分别在边AD,AB上,连接CE,CF,且满足∠DCE=∠BCF,BF=DE,∠A=60°,连接EF.
(1)若EF=2,求△AEF的面积;
(2)如图2,取CE的中点P,连接DP,PF,DF,求证:DP⊥PF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( )

A. 24m B. 22m C. 20m D. 18m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com