
����Ŀ����ƽ��ֱ������ϵ�У��� A����2��0����B��2��0����C��0��2������ D����E�ֱ��� AC��BC���е㣬����CDE�Ƶ�C��ʱ����ת�õ���CD��E��������ת��Ϊ�������� AD����BE����
��1����ͼ������ 0��������90������ AD���CE��ʱ�������Ĵ�С��
��2����ͼ������ 90��������180�������� D�������߶� BE����ʱ���� sin��CBE����ֵ��
��3����ֱ��AD����ֱ��BE���ཻ�ڵ�P�����P�ĺ�����m��ȡֵ��Χ��ֱ��д�������������

���𰸡���1��60�㣻��2��![]() ����3����
����3����![]() ��m��
��m��![]() ��
��
�����������������(1)��ͼ1�У�����ƽ���ߵ����ʿɵá�AD��C=��E��CD��=90�㣬�ٸ���AC=2CD�䣬�Ƴ���CAD��=30�㣬�ɴ˼��ɽ�������� (2)��ͼ2�У���CK��BE����K�����ݹ��ɶ����͵���ֱ�������ε��������CK�ij����ٸ���sin��CBE��= ![]() �����ɽ��������(3)����ͼ3��ͼ4�ֱ������P����������ֵ�Լ���Сֵ���ɽ������.
�����ɽ��������(3)����ͼ3��ͼ4�ֱ������P����������ֵ�Լ���Сֵ���ɽ������.
���������
��1����ͼ1�У�
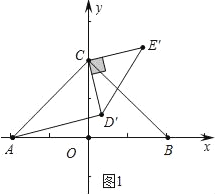
��AD���CE�䣬
���AD��C=��E��CD��=90�㣬
��AC=2CD�䣬
���CAD��=30�㣬
���ACD��=90�㩁��CAD��=60�㣬
���=60�㣮
��2����ͼ2�У���CK��BE����K��
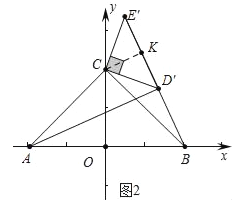
��AC=BC= ![]() =2
=2 ![]() ��
��
��CD��=CE��= ![]() ��
��
�ߡ�CD��E���ǵ���ֱ�������Σ�CD��=CE��= ![]() ��
��
��D��E��=2��
��CK��D��E�䣬
��KD��=E��K��
��CK= ![]() D��E��=1��
D��E��=1��
��sin��CBE��= ![]() =
= ![]() =
= ![]() ��
��
��3����ͼ3�У���CΪԲ��![]() Ϊ�뾶����C����BE�����C����ʱAP������ı���CD��PE���������Σ���PH��AB��H��
Ϊ�뾶����C����BE�����C����ʱAP������ı���CD��PE���������Σ���PH��AB��H��
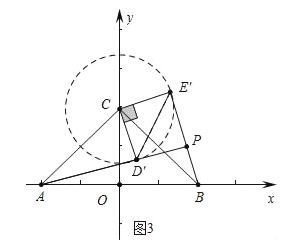
��AP=AD��+PD��= ![]() +
+ ![]() ��
��
��cos��PAB= ![]() =
= ![]() ��
��
��AH=2+ ![]() ��
��
���P����������ֵΪ![]() ��
��
��ͼ4�У���BE�����C����ʱAP��̣����ı���CD��PE���������Σ���PH��AB��H��
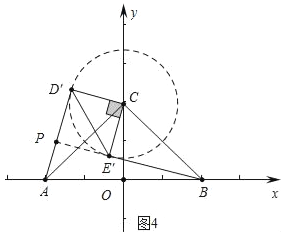
���ݶԳ��Կ�֪OH= ![]() ��
��
���P���������СֵΪ��![]() ��
��
���P�������ȡֵ��ΧΪ��![]() ��m��
��m��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
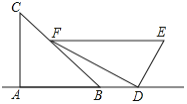
����Ŀ������˼����С��ͬѧ����һ����ѧ��У���һ��ֱ�����ǰ���ͼ���ã�![]() ��
��![]() ��
��![]() ��ͬһֱ���ϣ���
��ͬһֱ���ϣ���![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧҪ����![]() ��
��![]() ���صľ��룬��
���صľ��룬��![]() ��
��![]() ֮����һˮ�أ�����ֱ�Ӳ�������������
֮����һˮ�أ�����ֱ�Ӳ�������������![]() ��
��![]() ͬһˮƽ����ѡȡ��һ��
ͬһˮƽ����ѡȡ��һ��![]() ����
����![]() ��ֱ�ӵ���
��ֱ�ӵ���![]() ��
��![]() ���أ��������õ�
���أ��������õ�![]() �ף�
�ף�![]() �ף�
�ף�![]() ���������С��ͬѧ���
���������С��ͬѧ���![]() ��
��![]() ����֮��ľ��룮
����֮��ľ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ƽ��ֱ������ϵ�а�ͼ�м�ͷ��ʾ�����˶�����1�δ�ԭ���˶����㣨1��1������2�ν����˶����㣨2��0������3�ν����˶����㣨3��2�������������������˶����ɣ�������2019���˶�����P�������ǣ�������

A. ��2018��1��B. ��2018,0��C. ��2019,2�� D. ��2019,1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
(1)(��3)0��(![]() )��2+(��1)2n
)��2+(��1)2n
(2)(m2)n(mn)3��mn��2
(3)x(x2��x��1)
(4)(��3a)2a4+(��2a2)3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ������ѵ���������ij�д�ȫ�о��꼶ѧ���������ȡ����ѧ��������һ��������Ŀ���ԣ��Ѳ��Խ����Ϊ�ĸ��ȼ���A����B����C����D�����������Ǹ����Խ�����������������������ͳ��ͼ�������ͳ��ͼ�е���Ϣ����������⣺

��1�����γ������Ե�ѧ���������� ����
��2������ͼ�С����Ķ������� ������������ͳ��ͼ����������
��3����A��B��C��D�ĸ��ȼ����θ���Ϊ90��75��65��55����λ���֣������磺�ȼ�ΪA��ͬѧ�����÷�Ϊ90�֣������������ƣ����о��꼶����ѧ��32000�������ȫ���μ�����������ԣ����Ƹ��о��꼶������60�����£�ѧ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����![]() �����豸����֪ÿ̨
�����豸����֪ÿ̨![]() ���豸�ijɱ���
���豸�ijɱ���![]() ���豸��1��5������˾��Ͷ��6��Ԫ����
���豸��1��5������˾��Ͷ��6��Ԫ����![]() ���豸��Ͷ��15��Ԫ����
���豸��Ͷ��15��Ԫ����![]() ���豸��������������豸��40̨�������������⣺
���豸��������������豸��40̨�������������⣺
��1��![]() �����豸ÿ̨�ijɱ��ֱ��Ƕ�����Ԫ��
�����豸ÿ̨�ijɱ��ֱ��Ƕ�����Ԫ��
��2����![]() �����豸ÿ̨���ۼ۷ֱ���5000Ԫ��9000Ԫ����˾�������������豸��50̨��������
�����豸ÿ̨���ۼ۷ֱ���5000Ԫ��9000Ԫ����˾�������������豸��50̨��������![]() ���豸��������10̨���ƻ����ۺ����������12��Ԫ�����ʲ�����������������˾���������������������
���豸��������10̨���ƻ����ۺ����������12��Ԫ�����ʲ�����������������˾���������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ij����������У���Ա�״����ŵײ����ĵ�O����ǰ��10m��������ţ������������߷������������ߣ�������������߶�Ϊ3mʱ�ﵽ��ߵ㣬��ʱ������е�ˮƽ����Ϊ6m����֪���ŵĺ�����Ϊ2.44m��
��1������ͼ��ʾ��ƽ��ֱ������ϵ�У��ʴ˷��������ܷ�����ţ����������������
��2������Ա��վ�ھ�������2m����������ʱ�ֵ��������Ϊ2.52m��������ֹ��Ա�Ĵ˴�������������ܣ������ٺ��˶�Զ������ֹ��Ա�����ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ���x2+y2+2x-4y+5=0,��x��y.
�⣺��x2+y2+2x-4y+5=0����x2+2x+1��+��y2-4y+4��=0
�ࣨx+1��2+��y-2��2=0 �ࣨx+1��2=0����y-2��2=0
��x=-1,y=2.
������Ĺ۲죬̽����������⣺
��֪����ͼ,����ABC��,��A����B����C���Եı߷ֱ�Ϊa��b��c,��E��AC���ϵ�һ������(��E���A��C���غ�).
(1)��a��b����a2+b216a12b+100=0,��c�Dz���ʽ��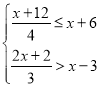 ����������⣬������ABC�����߳���
����������⣬������ABC�����߳���
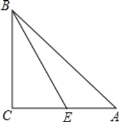
(2)��(1)�������õ��������ABC�У�����AE=m����m����ʲô����ʱ��BE����ABC���ܳ��ֳ������ֵIJС��2?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com