
【题目】阅读材料:若x2+y2+2x-4y+5=0,求x、y.
解:∵x2+y2+2x-4y+5=0,(x2+2x+1)+(y2-4y+4)=0
∴(x+1)2+(y-2)2=0 ∴(x+1)2=0,(y-2)2=0
∴x=-1,y=2.
根据你的观察,探究下面的问题:
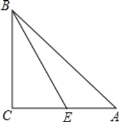
已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).
(1)当a、b满足a2+b216a12b+100=0,且c是不等式组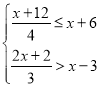 的最大整数解,试求△ABC的三边长;
的最大整数解,试求△ABC的三边长;
(2)在(1)的条件得到满足的△ABC中,若设AE=m,则当m满足什么条件时,BE将△ABC的周长分成两部分的差不小于2?
【答案】(1)a=8,b=6,c=10;(2)m≥3或m≤1.
【解析】
(1)根据a2+b2-16a-12b+100=0,且c是不等式组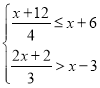 的最大整数解,可以分别求得a、b、c的值;
的最大整数解,可以分别求得a、b、c的值;
(2)由题意可得|(AB+AE)-(BC+CE)|≥2,可以得到关于m的不等式,从而可以解答本题.
(1)∵a2+b2-16a-12b+100=0,
∴(a-8)2+(b-6)2=0,
∴a-8=0,b-6=0,
得a=8,b=6,
解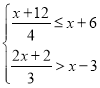 得,-4≤x<11,
得,-4≤x<11,
∵c是不等式组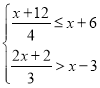 的最大整数解,
的最大整数解,
∴c=10,
∴a=8,b=8,c=10;
(2)由题意可得,
|(AB+AE)-(BC+CE)|≥2,
即|(10+m)-(8+6-m)|≥2,
解得,m≥3或m≤1,
即当m≥3或m≤1时,BE分△ABC的周长的差不小于2.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
(1)如图①,若 0°<α<90°,当 AD′∥CE′时,求α的大小;
(2)如图②,若 90°<α<180°,当点 D′落在线段 BE′上时,求 sin∠CBE′的值;
(3)若直线AD′与直线BE′相交于点P,求点P的横坐标m的取值范围(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线![]() 过点D,B,C三点.
过点D,B,C三点.

(1)求抛物线的解析式;
(2)求证:ED是⊙P的切线;
(3)若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线![]() 上吗?请说明理由;
上吗?请说明理由;
(4)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(1)求A点坐标及线段AB的长;
(2)若点P由点A出发以每秒1个单位的速度沿AB边向点B移动,1秒后点Q也由点A出发以每秒7个单位的速度沿A-O-C-B的方向向点B移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒.
①当PQ⊥AC时,求t的值;
②当PQ∥AC时,对于抛物线对称轴上一点H,当点H的纵坐标满足条件_________时,∠HOQ<∠POQ.(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
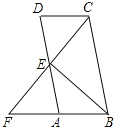
【题目】如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=100°,求∠ABE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BA=BC,∠BAC=α,M是AC的中点,P是线段BM上的动点,将线段PA绕点P顺时针旋转2α得到线段PQ.
(1)若α=60°,且点P与点M重合(如图1),线段CQ的延长线交射线BM于点D,此时∠CDB的度数为________
(2)在图2中,点P不与点B、M重合,线段CQ的延长线交射线BM于点D,则∠CDB的度数为(用含α的代数式表示)________.
(3)对于适当大小的α,当点P在线段BM上运动到某一位置(不与点B、M重合)时,能使得线段CQ的延长线与射线BM交于点D,且PQ=DQ,则α的取值范围是________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展了“手机伴我行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成图①、图②不完整的统计图,已知问卷调查中“查资料”的人数是40人,条形统计图中“0~1表示每周使用手机的时间大于0小时而小于或等于1小时,以此类推.

(1)本次问卷调查一共调查了多少名学生?
(2)补全条形统计图;
(3)该校共有学生1200人,估计每周使用手机“玩游戏”是多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
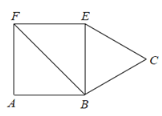
【题目】如图,正方形 ABEF 的面积为 4,△BCE 是等边三角形,点 C 在正方形ABEF 外,在对角线 BF 上有一点 P,使 PC+PE 最小,则这个最小值的平方为( )
A.![]() B.
B.![]() C.12D.
C.12D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
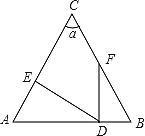
【题目】如图∠A=∠B,∠C=![]() ,DE⊥AC于点E,FD⊥AB于点D.
,DE⊥AC于点E,FD⊥AB于点D.
(1)若∠EDA=25°,则∠EDF=________°;
(2)若∠A=65°,则∠EDF=_______°;
(3)若![]() =50°,则∠EDF=_______°;
=50°,则∠EDF=_______°;
(4)若∠EDF=65°,则![]() _______°;
_______°;
(5)∠EDF与![]() 的关系为_______.
的关系为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com