
 如图,已知直角梯形OABC的A点在x轴上,C点在y轴上,OC=6,OA=OB=10,PQ∥AB交AC于D点,且∠ODQ=90°,求D点的坐标.
如图,已知直角梯形OABC的A点在x轴上,C点在y轴上,OC=6,OA=OB=10,PQ∥AB交AC于D点,且∠ODQ=90°,求D点的坐标. 解:连接BO,延长OD,交AB于E,
解:连接BO,延长OD,交AB于E,| OB2-OC2 |
| 1 |
| 3 |
| 1 |
| 3 |
|
|
| 3 |
| 5 |
|
|
| 45 |
| 7 |
| 15 |
| 7 |


科目:初中数学 来源: 题型:
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
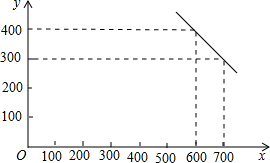 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量(件)与销售单价x(元/件)可近似看做-次函数y=kx+b的关系,如图所示.
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量(件)与销售单价x(元/件)可近似看做-次函数y=kx+b的关系,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,双曲线y1=
如图,双曲线y1=| 4 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,P为∠AOB内一点,PC⊥OA于点C,PD⊥OB于点D,PC=PD,连结OP,可通过证明△POC≌△POD得∠AOP=∠BOP.适用的判定定理是( )
如图,P为∠AOB内一点,PC⊥OA于点C,PD⊥OB于点D,PC=PD,连结OP,可通过证明△POC≌△POD得∠AOP=∠BOP.适用的判定定理是( )| A、SAS | B、ASA |
| C、SSS | D、HL |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com