
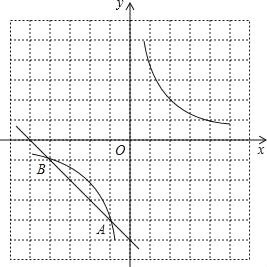
【题目】如图,在方格纸中(小正方形的边长为1),反比例函数的图象与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(1)求这个反比例函数的解析式;
(2)若点C在已知的反比例函数的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标.
【答案】(1)y=![]() (2)(2,2)或(﹣2,﹣2)
(2)(2,2)或(﹣2,﹣2)
【解析】
(1)设这个反比例函数的解析式是y=![]() ,把A点的坐标代入,即可求出答案;
,把A点的坐标代入,即可求出答案;
(2)设C点的坐标为(x,![]() ),根据两点之间距离公式和AC=BC得出方程,求出x即可.
),根据两点之间距离公式和AC=BC得出方程,求出x即可.
(1)设这个反比例函数的解析式是y=![]() ,
,
由图象可知:点A的坐标为(﹣1,﹣4),
代入得:k=4,
所以这个反比例函数的解析式是y=![]() ;
;
(2)设C点的坐标为(x,![]() ),
),
∵A(﹣1,﹣4),B(﹣4,﹣1),AC=BC,
∴根据两点之间距离公式得:(﹣1﹣x)2+(﹣4﹣![]() )2=(﹣4﹣x)2+(﹣1﹣
)2=(﹣4﹣x)2+(﹣1﹣![]() )2,
)2,
解得:x=±2,
当x=2时,![]() =2;
=2;
当x=﹣2时,![]() =﹣2,
=﹣2,
所以点C的坐标为(2,2)或(﹣2,﹣2).


科目:初中数学 来源: 题型:
【题目】星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(m)与散步所用时间t(min)之间的函数关系,依据图象,下面描述中符合小红散步情景的有_____(填序号)
①从家里出发,到了一个公共阅报栏,看了一会儿报后,继续向前走了一段然后回家了
②小红家距离公共阅报栏300m
③从家出发,一直散步(没有停留),然后回家了
④小红本次散步共用时18min

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如图统计图.
请根据图中提供的信息,解答下列问题:
(1)所抽取的样本容量为 .
(2)若抽取的学生成绩用扇形图来描述,则表示“第三组(79.5~89.5 )”的扇形的圆心角度数为多少?
(3)如果成绩在80分以上(含80分)的同学可以获奖,请估计该校有多少名同学获奖.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①为平地上一幢建筑物与铁塔图,图②为其示意图.建筑物AB与铁塔CD都垂直于地面,BD=20m,在A点测得D点的俯角为45°,测得C点的仰角为58°.求铁塔CD的高度.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)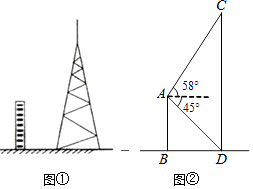
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E,F分别是AC,AB边上点,连接EF,将纸片ACB的一角沿EF折叠.
(1)如图①,若折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△AEF , 则AE=;
(2)如图②,若折叠后点A落在BC边上的点M处,且使MF∥CA.求AE的长;
(3)如图③,若折叠后点A落在BC延长线上的点N处,且使NF⊥AB.求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
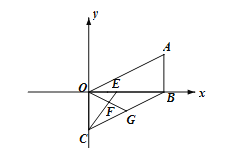
【题目】(12分)已知,在平面直角坐标系中,AB⊥x轴于点B,点A(a,b)满足![]() +|b-2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.
+|b-2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.
(1)则a=____,b=____;点C坐标为________;
(2)如下图所示:点D(m, n)在线段BC上,求m、n满足的关系式;

(3)如下图所示:E是线段OB上一动点,以OB为边作∠G=∠AOB,,交BC于点G,连CE交OG于点F,的当点E在线段OB上运动过程中, ![]() 的值是否会发生变化?若变化请说明理由,若不变,请求出其值.
的值是否会发生变化?若变化请说明理由,若不变,请求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成4 个小长方形,然后按图2的形状拼成一个正方形.

(1)图2中阴影部分的面积为 ;
(2)观察图2,请你写出式子(m+n)2,(m-n)2,mn之间的等量关系: ;
(3)若x+y=-6,xy=2.75,求x-y的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:EF∥AD,∠1=∠2,∠B=55°,求∠BDG的大小.

请同学们在下面的横线上把解答过程补充完整:
解:∵ EF//AD, (已知)
∴ ∠2=∠3, ( )
又∵ ∠1=∠2, (已知)
∴ ∠1=∠3, (等量代换)
∴ ,(内错角相等,两直线平行)
∴ ∠B+∠BDG=180°, ( )
∵ ∠B=55°, (已知)
∴ ∠BDG = .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com