
【题目】图①为平地上一幢建筑物与铁塔图,图②为其示意图.建筑物AB与铁塔CD都垂直于地面,BD=20m,在A点测得D点的俯角为45°,测得C点的仰角为58°.求铁塔CD的高度.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)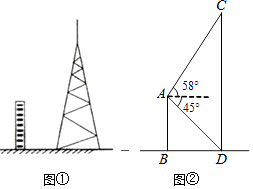
【答案】解:如图,过点A作AE⊥CD,垂足为E,
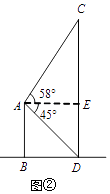
则四边形ABDE矩形,
∵BD=20m,在A点测得D点的俯角为45°,在测得C点的仰角为58°,
∴∠ADB=∠EAD=45°,
∴AB=ED=BD=20m,
在Rt△AEC中,tan∠CAE= ![]() ,
,
∴tan58°= ![]() =
= ![]() ,
,
∴CE=20 tan58°=20×1.60=32,
∴CD=CE+ED=32+20=52米.
答:铁塔CD的高度为52米.
【解析】先过点A作AE⊥CD,垂足为E,则四边形ABDE矩形,根据∠ADB=∠EAD=45°,可得AB=ED=BD=20m,在Rt△AEC中,根据正切定义得出tan∠CAE,求得CE的长,进而得到铁塔CD的高度.
【考点精析】掌握关于仰角俯角问题是解答本题的根本,需要知道仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,过点P(2,2![]() )作x轴的平行线交y轴于点A,交双曲线y=
)作x轴的平行线交y轴于点A,交双曲线y=![]() (x>0)于点N,作PM⊥AN交双曲线y=
(x>0)于点N,作PM⊥AN交双曲线y=![]() (x>0)于点M,连接AM,若PN=4.
(x>0)于点M,连接AM,若PN=4.
(1)求k的值;
(2)设直线MN解析式为y=ax+b,求不等式![]()
![]() ax+b的解集.
ax+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个正整数a可以表示为连续的两个奇数的平方差的形式,如:8=32﹣12,16=52﹣32,24=72﹣52,……,我们则称形如8,16,24这样的正整数a为“奇特数”.
(1)请写出最小的三位“奇特数”,并表示成连续的两个奇数的平方差的形式;
(2)求证:任意一个“奇特数”都是8的倍数;
(3)若一个三位数b为“奇特数”,其百位和个位上的数字相同,十位上的数字比个位上的数字大m(m为正整数),求满足条件的所有三位“奇特数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
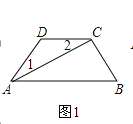
【题目】(1)如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明;
(2)如图,AB∥CD,AB的下方两点E、F满足:BF平分∠ABE、DF平分∠CDE,若∠DFB=20°,∠CDE=70°,求∠ABE的度数;
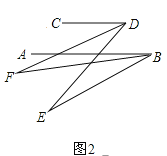
(3)在前面的条件下,若P是BE上一点,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变,可以证明只有一个是正确的,请你作出正确的选择并求值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】细观察,找规律.
下列各图中的![]() 与
与![]() 平行.
平行.

![]() 图
图![]() 中的
中的![]() ______ 度,
______ 度,
图![]() 中的
中的![]() ______ 度,
______ 度,
图![]() 中的
中的![]() ______ 度,
______ 度,
图![]() 中的
中的![]() ______ 度,
______ 度,
![]() ,
,
第![]() 个图中的
个图中的![]() ______ 度
______ 度
![]() 第n个图中的
第n个图中的![]() ______
______
![]() 请你证明图
请你证明图![]() 的结论.
的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
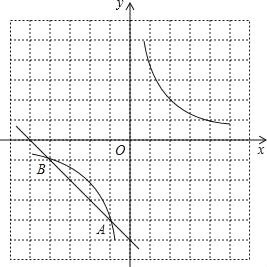
【题目】如图,在方格纸中(小正方形的边长为1),反比例函数的图象与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(1)求这个反比例函数的解析式;
(2)若点C在已知的反比例函数的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,0),B(2,0),点C在y轴上,且S△ABC=3.
(1)求点C的坐标;
(2)以点A、B、C为顶点,作长方形,试写出该长方形第四个顶点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,FG∥EB,
中,FG∥EB,![]() ,那么
,那么![]() 等于多少度?为什么?
等于多少度?为什么?

解:![]() =_______________.
=_______________.
因为![]() ∥
∥![]() (______________________),
(______________________),
所以![]() (_________________________________).
(_________________________________).
因为![]() (已知),
(已知),
所以![]() (_____________________).
(_____________________).
所以DE∥BC(_____________________).
所以![]() =_________(____________________).
=_________(____________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com